2022-2023學年北京十九中九年級（上）假期反饋數學試卷

一、選擇題（每題3分，共24分）

• 1．下列二次根式中，能與

  3

  合并的是（　　）

  A． 18

  B． 1 3

  C． 24

  D． 0 . 3
  組卷：96引用：6難度：0.9

  解析

• 2．下列四選項中，以三個實數為邊長，能構成直角三角形的是（　　）

  A． 3 ，2， 5

  B． 1 ， 2 ， 3

  C． 6 ， 8 ， 10

  D．3，4，6
  組卷：73引用：2難度：0.9

  解析

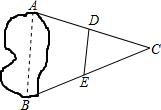• 3．如圖，A、B兩點分別位于一個池塘的兩端，小明想用繩子測量A，B間的距離，但繩子不夠長，一位同學幫他想了一個主意：先在地上取一個可以直接到達A，B的點C，找到AC，BC的中點D，E，并且測出DE的長為10m,則A，B間的距離為（　　）

  A．15m

  B．20m

  C．25m

  D．30m
  組卷：611引用：15難度：0.9

  解析

• 4．下列圖形中的曲線不表示y是x的函數的是（　　）

  A．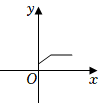

  B．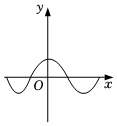

  C．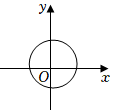

  D．
  組卷：455引用：1難度：0.7

  解析

• 5．若點（-4，y₁），（2，y₂）都在直線y=

  -

  1

  3

  x

  +

  t

  上，則y₁與y₂的大小關系是（　　）

  A．y1＞y2

  B．y1=y2

  C．y1＜y2

  D．無法確定
  組卷：586引用：13難度：0.9

  解析

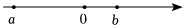• 6．實數a、b在數軸上的位置如圖所示，且|a|＞|b|，則化簡

  a

  2

  -

  |

  a

  +

  b

  |

  的結果為（　　）

  A．2a+b

  B．-2a+b

  C．b

  D．2a-b
  組卷：2847引用：82難度：0.9

  解析

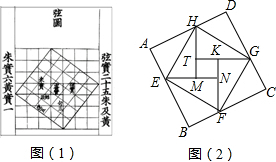• 7．我國漢代數學家趙爽為了證明勾股定理，創制了一幅“弦圖”，后人稱其為“趙爽弦圖”（如圖（1）所示）．圖（2）由弦圖變化得到，它是由八個全等的直角三角形拼接而成的．記圖中正方形ABCD，正方形EFGH，正方形MNKT的面積分別為S₁，S₂，S₃，若S₁+S₂+S₃=72，則S₂的值是（　　）

  A．48

  B．36

  C．24

  D．25
  組卷：419引用：4難度：0.3

  解析

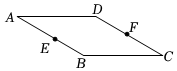• 8．如圖，菱形ABCD中，∠A=30°，AB=4，點E，F分別是邊AB，CD的中點，動點P從點E出發，按逆時針方向，沿EB，BC，CF勻速運動到點F停止，設△PAD的面積為S，動點P運動的路徑總長為x,能表示S與x函數關系的圖象大致是
  （　　）

  A．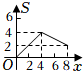

  B．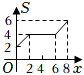

  C．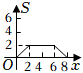

  D．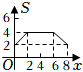
  組卷：372引用：5難度：0.7

  解析

二、填空題（每題2分，共16分）

• 9．函數y=

  x

  -

  2

  x

  -

  3

  中，自變量x的取值范圍是

  ．
  組卷：4187引用：71難度：0.9

  解析

四、解答題（19題4分，20題5分，21題4分，22-23題5分，24題8分，25題5分，26題6分，27題6分）

• 26．在平面直角坐標系xOy中，一次函數y=kx+b（k≠0）的圖象過點A（2，3），B（0，-1），點B關于x軸的對稱點為C．
  （1）求這個一次函數的表達式；
  （2）點D為x軸上任意一點，求線段AD與線段CD之和的最小值；
  （3）一次函數y=ax+c（a≠0）的圖象經過點C，當x＞2時，對于x的每一個值，y=ax+c的值都小于y=kx+b的值，直接寫出a的取值范圍．
  組卷：505引用：4難度：0.5

  解析

• 27．在正方形ABCD中，P是射線CB上的一個動點，過點C作CE⊥AP于點E，射線CE交直線AB于點F，連接BE．
  
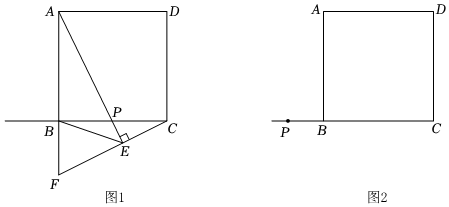
  （1）如圖1，當點P在線段CB上時（不與端點B，C重合）．
  ①求證：∠BCF=∠BAP；
  ②求證：EA=EC+

  2

  EB；
  （2）如圖2，當點P在線段CB的延長線上時（BP＜BA），依題意補全圖2并用等式表示線段EA，EC，EB之間的數量關系．
  組卷：1775引用：8難度：0.2

  解析