2023-2024學(xué)年四川省成都市青羊區(qū)石室陽安中學(xué)高三（上）開學(xué)數(shù)學(xué)試卷（理科）

一、單選題

• 1．設(shè)集合S=

  {

  x

  |

  x

  ＞

  -

  1

  2

  }

  ，T={x|2^3x-1＜1}，則S∩T=（　　）

  A．?

  B． { x | x ＜ - 1 2 }

  C． { x | x ＞ 1 3 }

  D． { x | - 1 2 ＜ x ＜ 1 3 }
  組卷：243引用：6難度：0.8

  解析

• 2．在復(fù)平面內(nèi)，復(fù)數(shù)z對(duì)應(yīng)的點(diǎn)的坐標(biāo)為（-2，-1），則

  z

  i

  =（　　）

  A．-1-2i

  B．-2-i

  C．-1+2i

  D．2-i
  組卷：256引用：5難度：0.8

  解析

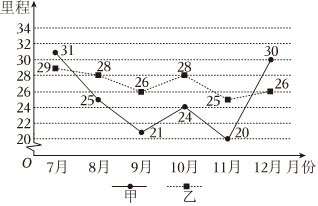• 3．走路是最簡單優(yōu)良的鍛煉方式，它可以增強(qiáng)心肺功能，血管彈性，肌肉力量等，甲、乙兩人利用手機(jī)記錄了去年下半年每個(gè)月的走路里程（單位：公里），現(xiàn)將兩人的數(shù)據(jù)繪制成如圖所示的折線圖，則下列結(jié)論中正確的是（　　）

  A．甲走路里程的極差等于10

  B．乙走路里程的中位數(shù)是26

  C．甲下半年每月走路里程的平均數(shù)小于乙下半年每月走路里程的平均數(shù)

  D．甲下半年每月走路里程的標(biāo)準(zhǔn)差小于乙下半年每月走路里程的標(biāo)準(zhǔn)差
  組卷：51引用：4難度：0.7

  解析

• 4．若實(shí)數(shù)x,y滿足約束條件

  y + 1 ≥ 0

  2 x + y - 4 ≤ 0

  x - 2 y + 3 ≥ 0

  ，則z=3y-x的最大值為（　　）

  A．- 1 2

  B．2

  C．5

  D．8
  組卷：81引用：4難度：0.6

  解析

• 5．下列命題正確的是（　　）

  A．命題“p∧q”為假命題，則命題p與命題q都是假命題

  B．命題“若x=y,則sinx=siny”的逆否命題為真命題

  C．若x0 使得函數(shù)f（x）的導(dǎo)函數(shù)f’（x0）=0，則x0為函數(shù)f（x）的極值點(diǎn)；?

  D．命題“?x0∈R，使得x02+x0+1＜0”的否定是：“?x∈R，均有x2+x+1＜0”
  組卷：51引用：6難度：0.8

  解析

• 6．已知中心在原點(diǎn)，焦點(diǎn)在y軸上的雙曲線的離心率為

  5

  ，則它的漸近線方程為（　　）

  A．y=±2x

  B．y=± 5 2 x

  C．y=± 1 2 x

  D．y=± 6 x
  組卷：331引用：11難度：0.9

  解析

• 7．把一個(gè)鐵制的底面半徑為4，側(cè)面積為

  16

  3

  π

  的實(shí)心圓柱熔化后鑄成一個(gè)球，則這個(gè)鐵球的表面積為（　　）

  A．16π

  B．12π

  C．24π

  D．9π
  組卷：165引用：4難度：0.5

  解析

三、解答題

• 22．在平面直角坐標(biāo)系xOy中，曲線

  C

  1

  ：

  x = cosφ

  y = - 1 + sinφ

  （φ為參數(shù)），以坐標(biāo)原點(diǎn)為極點(diǎn)，x軸的正半軸為極軸建立極坐標(biāo)系，曲線C₂的極坐標(biāo)方程為ρ=2cosθ．
  （1）寫出曲線C₁的極坐標(biāo)方程，曲線C₂的直角坐標(biāo)方程；
  （2）設(shè)點(diǎn)M的極坐標(biāo)為M（2，0），射線

  θ

  =

  α

  （

  -

  π

  4

  ＜

  α

  ＜

  0

  ，

  ρ

  ≥

  0

  ）

  與曲線C₁、C₂分別交于A、B兩點(diǎn)（異于極點(diǎn)），當(dāng)

  ∠

  AMB

  =

  π

  4

  時(shí)，求線段AB的長．
  組卷：139引用：4難度：0.5

  解析

• 23．設(shè)f（x）=|x-3|+|x-4|．
  （1）解不等式f（x）≤2；
  （2）已知實(shí)數(shù)x、y、z滿足2x²+3y²+6z²=a（a＞0），且x+y+z的最大值是1，求a的值．
  組卷：518引用：5難度：0.5

  解析