2023-2024學年甘肅省張掖市民樂一中高三（上）第一次診斷數學試卷

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的4個選項中，只有1項是符合題目要求的．

• 1．已知M，N均為R的子集，且?_RM?N，則M∪（?_RN）=（　　）

  A．?

  B．M

  C．N

  D．R
  組卷：923引用：17難度：0.8

  解析

• 2．祖暅原理：“冪勢既同，則積不容異”．它是中國古代一個涉及幾何體體積的問題，意思是兩個同高的幾何體，如在等高處的截面積恒相等，則體積相等．設A，B為兩個同高的幾何體，p：A，B的體積相等，q：A，B在等高處的截面積恒相等，根據祖暅原理可知，q是p的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：120引用：5難度：0.9

  解析

• 3．在平面直角坐標系xOy中，角α和角β的頂點均與原點O重合，始邊均與x軸的非負半軸重合，它們的終邊關于直線y=x對稱，若

  cosα

  =

  2

  3

  ，則sinβ=（　　）

  A． - 5 3

  B． - 2 3

  C． 2 3

  D． 5 3
  組卷：89引用：3難度：0.8

  解析

• 4．若將函數y=3sin（2x+

  π

  3

  ）+

  1

  2

  的圖象向右平移

  π

  6

  個單位長度，則平移后圖象的對稱中心為（　　）

  A．（ kπ 2 + π 4 ， 1 2 ）（k∈Z）	B．（ kπ 2 + π 4 ，0）（k∈Z）
  C．（ kπ 2 ， 1 2 ）（k∈Z）	D．（ kπ 2 ，0）（k∈Z）
  組卷：3引用：2難度：0.7

  解析

• 5．已知函數f（x）=

  x 2 + 2 x , x ≥ 0

  2 x - x 2 ， x ＜ 0

  ．若f（2-a²）＞f（a），則實數a的取值范圍是（　　）

  A．（-∞，-2）∪（1，+∞）	B．（-1，1）
  C．（-2，1）	D．（-1，2）
  組卷：268引用：5難度：0.9

  解析

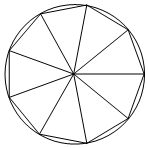• 6．割圓術的核心思想是將一個圓的內接正n邊形等分成n個等腰三角形（如圖所示），當n變得很大時，這n個等腰三角形的面積之和近似等于圓的面積．運用割圓術的思想得到sin3°的近似值為（　　）

  A． π 90

  B． π 180

  C． π 270

  D． π 60
  組卷：9引用：2難度：0.7

  解析

• 7．已知曲線f（x）=e^x在點P（0，f（0））處的切線也是曲線g（x）=ln（ax）的一條切線，則a的值為（　　）

  A． e 3

  B． e 2

  C．e2

  D． e 3 3
  組卷：102引用：3難度：0.6

  解析

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

• 21．已知函數f（x）=lnx-x²．
  （I）求函數f（x）的單調遞增區間；
  （II）求函數f（x）在（0，a]（a＞0）上的最大值．
  組卷：23引用：5難度：0.3

  解析

• 22．設函數f（x）=

  1

  -

  a

  2

  x²+ax-lnx,（a∈R）．
  （1）當a=1時，求函數f（x）的極值；
  （2）若對任意a∈（4，5）及任意x₁，x₂∈[1，2]，恒有“

  a

  -

  1

  2

  m+ln2＞|f（x₁）-f（x₂）|成立，求實數m的取值范圍．
  組卷：158引用：3難度：0.3

  解析