2011-2012學年山東省淄博市周村二中高三（上）開學數學試卷

一、選擇題：本大題共12小題．每小題5分，共60分在每小題給出的四個選項中，只有一項是滿足題目要求的.

• 1．已知集合A={0，1，2，3，4，5，6}，集合B={x|x=3a,a∈A}，則A∩B=（　　）

  A．{3，6}

  B．{0，3，6}

  C．{0，2，6}

  D．{0，3}
  組卷：1引用：1難度：0.9

  解析

• 2．若復數z滿足

  z

  -

  3

  （

  1

  +

  z

  ）

  i

  =

  1

  ，則z+z²的值等于（　　）

  A．1

  B．0

  C．-1

  D． - 1 2 + 3 2 i
  組卷：10引用：2難度：0.9

  解析

• 3．設

  OM

  =（1，

  1

  2

  ），

  ON

  =（0，1），則滿足條件0≤

  OP

  ?

  ON

  ≤1，

  0

  ≤

  OP

  ?

  OM

  ≤

  1

  的動點P的變化范圍（圖中陰影部分含邊界）是（　　）

  A．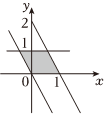

  B．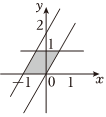

  C．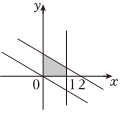

  D．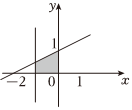
  組卷：99引用：6難度：0.7

  解析

• 4．下列函數中，最小正周期為π，且圖象關于直線

  x

  =

  π

  3

  對稱的是（　　）

  A． y = sin （ 2 x + π 6 ）	B． y = sin （ x 2 + π 3 ）
  C． y = sin （ 2 x - π 3 ）	D． y = sin （ 2 x - π 6 ）
  組卷：221引用：49難度：0.9

  解析

• 5．拋物線y²=2px的焦點與雙曲線

  x

  2

  3

  -y²=1的右焦點重合，則p的值為（　　）

  A．-2

  B．2

  C．-4

  D．4
  組卷：168引用：10難度：0.9

  解析

• 6．在△ABC中，角A、B、C所對的邊長分別為a、b、c,若

  C

  =

  120

  °

  ，

  c

  =

  2

  b

  ，則關系①B＞45°②A＞45°③b＞a④b＜a中正確的是（　　）

  A．①③

  B．②④

  C．①

  D．③
  組卷：19引用：1難度：0.7

  解析

• 7．設數列{a_n}滿足：a₁=2，a_n+1=1-

  1

  a

  n

  ，記數列{a_n}的前n項之積為Π_n，則Π₂₀₁₁的值為（　　）

  A．2

  B．-1

  C． 1 2

  D．1
  組卷：11引用：2難度：0.9

  解析

三、解答題：本大題共6小題，滿分74分．解答須寫出文字說明、證明過程和演算步驟

• 21．已知函數f（x）=x²+ax-lnx,a∈R．
  （1）若函數f（x）在[1，2]上是減函數，求實數a的取值范圍；
  （2）令g（x）=f（x）-x²，是否存在實數a,當x∈（0，e]（e是自然常數）時，函數g（x）的最小值是3，若存在，求出a的值；若不存在，說明理由；
  （3）當x∈（0，e]時，證明：

  e

  2

  x

  2

  -

  5

  2

  x

  ＞

  （

  x

  +

  1

  ）

  lnx

  ．
  組卷：3280引用：30難度：0.5

  解析

• 22．已知拋物線C：y²=4x的準線與x軸交于M點，過M點斜率為k的直線l與拋物線C交于A、B兩點（A在M、B之間）．
  （1）F為拋物線C的焦點，若|AM|=

  5

  4

  |AF|，求k的值；
  （2）如果拋物線C上總存在點Q，使得QA⊥QB，試求k的取值范圍．
  組卷：42引用：7難度：0.3

  解析