2022年福建省莆田二中高考數學模擬試卷（四）

一、單項選擇題。本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．已知集合A={x∈N|-1≤x≤1}，B={x|x²-x-2≤0}，則A∩B的子集個數為（　　）

  A．2

  B．3

  C．4

  D．8
  組卷：95引用：1難度：0.9

  解析

• 2．如圖，在復平面內，復數z₁，z₂對應的向量分別是

  OA

  ，

  OB

  ，則復數

  z

  1

  z

  2

  對應的點位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：391引用：26難度：0.9

  解析

• 3．若向量

  a

  =

  （

  m

  ,-

  3

  ）

  ，

  b

  =

  （

  3

  ，

  1

  ）

  ，則“m＜1”是“向量

  a

  ，

  b

  夾角為鈍角”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：1003引用：12難度：0.8

  解析

• 4．與直線x+2y+1=0垂直，且與圓x²+y²=5相切的直線方程是（　　）

  A．2x+y+ 5 =0或2x+y- 5 =0	B．2x+y+5=0或2x+y-5=0
  C．2x-y+ 5 =0或2x-y- 5 =0	D．2x-y+5=0或2x-y-5=0
  組卷：336引用：2難度：0.7

  解析

• 5．我國著名數學家華羅庚先生曾說：“數缺形時少直觀，形缺數時難入微，數形結合百般好，隔離分家萬事休．”在數學的學習和研究中，常用函數的圖像來研究函數的性質，也常用函數的解析式來琢磨函數圖像的特征，如函數

  f

  （

  x

  ）

  =

  x

  2

  +

  a

  |

  x

  |

  （a∈R）的圖像不可能是（　　）

  A．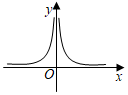

  B．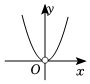

  C．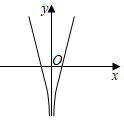

  D．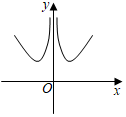
  組卷：225引用：10難度：0.6

  解析

• 6．小小的火柴棒可以拼成幾何圖形，也可以拼成數字．如圖所示，我們可以用火柴棒拼出1至9這9個數字：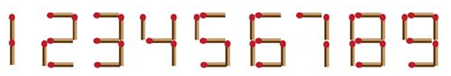
  
  比如：“1”需要2根火柴棒，“7”需要3根火柴棒．若用8根火柴棒以適當的方式全部放入的表格中（沒有放入火柴棒的空位表示數字“0”），那么最多可以表示無重復數字的三位數的個數為（　　）

  A．8

  B．12

  C．16

  D．20
  組卷：228引用：3難度：0.8

  解析

• 7．設拋物線E：y²=8x的焦點為F，過點M（4，0）的直線與E相交于A，B兩點，與E的準線相交于點C，點B在線段AC上，|BF|=3，則△BCF與△ACF的面積之比

  S

  △

  BCF

  S

  △

  ACF

  =（　　）

  A． 1 4

  B． 1 5

  C． 1 6

  D． 1 7
  組卷：736引用：9難度：0.5

  解析

四、解答題。本題共6小題，共70分,。解答應寫出文字說明、證明過程或演算步驟。

• 21．已知函數f（x）=ln（x+1）-ax+1（a∈R）．
  （1）當a＞0時，設函數f（x）的最大值為h（a），證明：h（a）≥1；
  （2）若函數

  g

  （

  x

  ）

  =

  f

  （

  x

  ）

  +

  1

  2

  x

  2

  有兩個極值點x₁，x₂（x₁＜x₂），求a的取值范圍，并證明：g（x₁）+g（x₂）＜2．
  組卷：459引用：4難度：0.5

  解析

• 22．已知橢圓

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  經過點

  （

  1

  ，

  3

  2

  ）

  ，離心率為

  1

  2

  ．
  （1）求橢圓C的方程；
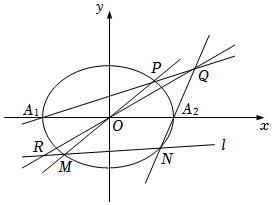
  （2）如圖，橢圓C的左、右頂點為A₁，A₂，不與坐標軸垂直且不過原點的直線l與C交于M，N兩點（異于A₁，A₂），點M關于原點O的對稱點為點P，直線A₁P與直線A₂N交于點Q，直線OQ與直線l交于點R．證明：點R在定直線上．
  組卷：214引用：2難度：0.4

  解析