2022-2023學年天津四十三中高三（上）期末數學試卷

一、選擇題（共9小題，每小題5分，滿分45分）

• 1．已知集合U={1，2，3，4，5，6}，A={2，4，5}，B={1，3，4，5}，則（?_UA）∩B=（　　）

  A．{1，2，3，6}	B．{4，5}
  C．{1，2，3，4，5，6}	D．{1，3}
  組卷：103引用：3難度：0.9

  解析

• 2．“x²＞4”是“x＞2”成立的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：565引用：4難度：0.8

  解析

• 3．函數f（x）=

  ln

  |

  x

  |

  x

  2

  +

  2

  的圖象大致為（　　）

  A．

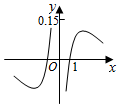
  B．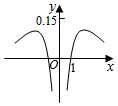

  C．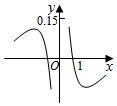

  D．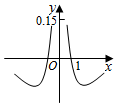
  組卷：4422引用：19難度：0.8

  解析

• 4．如圖是容量為500的樣本的頻率分布直方圖，那么樣本數據落在[10，14）內的頻率，頻數分別為（　　）
  

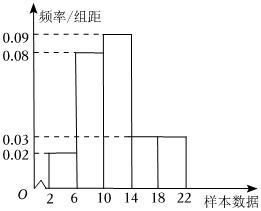
  A．0.32；120

  B．0.32；160

  C．0.09；45

  D．0.36；180
  組卷：268引用：3難度：0.8

  解析

• 5．設

  a

  =

  lo

  g

  3

  8

  ，

  b

  =

  2

  1

  .

  1

  ，

  c

  =

  0

  .

  8

  1

  .

  1

  ，則a,b,c的大小關系是（　　）

  A．b＜a＜c

  B．c＜b＜a

  C．c＜a＜b

  D．a＜c＜b
  組卷：229引用：3難度：0.7

  解析

• 6．棱長為1的正方體的頂點都在一個球的球面上，則該球的體積為（　　）

  A． 3 π 2

  B． 3 π 3

  C． 2 π 3

  D． π 3
  組卷：280引用：1難度：0.7

  解析

三、解答題（共5小題，滿分60分）

• 19．已知等比數列{a_n}的各項均為正數，2a₅，a₄，4a₆成等差數列，且滿足

  a

  4

  =

  4

  a

  2

  3

  ，等差數列數列{b_n}的前n項和S_n，b₂+b₄=6，S₄=10
  （1）求數列{a_n}和{b_n}的通項公式；
  （2）設

  c

  n

  =

  b n （ n 為奇數 ）

  a n ? b n （ n 為偶數 ）

  ，求數列{c_n}的前2n項和．
  （3）設

  d

  n

  =

  b

  2

  n

  +

  5

  b

  2

  n

  +

  1

  b

  2

  n

  +

  3

  a

  n

  ，

  n

  ∈

  N

  *

  ，

  {

  d

  n

  }

  的前n項和T_n，求證：

  T

  n

  ＜

  1

  3

  ．
  組卷：354引用：1難度：0.5

  解析

• 20．已知函數f（x）=xlnx,g（x）=（a+1）x-a.
  （1）求函數h（x）=f（x）-g（x）的極值；
  （2）若存在x∈[1，e]時，使2f（x）≥-x²+ax-3成立，求a的取值范圍；
  （3）若不等式h（x）≤（x-a-2）e^x-1+a對任意x∈[1，+∞）恒成立，求實數a的取值范圍．
  組卷：423引用：3難度：0.6

  解析