2019-2020學年河南省平頂山一中高三（下）開學數學試卷（文科）

一、選擇題、本大題共12小題，每小題5分，共60分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知集合A={1，2，3，6}，B={x|2^x＞4}，則A∩B=（　　）

  A．{6}

  B．{3，6}

  C．{1，2}

  D．{2，3，6}
  組卷：65引用：3難度：0.9

  解析

• 2．若復數z滿足z（1-2i）=10，則復數z在復平面內對應的點在（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：138引用：5難度：0.8

  解析

• 3．已知雙曲線C的兩條漸近線的夾角為60°，則雙曲線C的方程不可能為（　　）

  A． x 2 3 - y 2 = 1

  B． x 2 3 - y 2 9 = 1

  C． y 2 3 - x 2 12 = 1

  D． y 2 21 - x 2 7 = 1
  組卷：56引用：3難度：0.7

  解析

• 4．設向量

  m

  ，

  n

  滿足|

  m

  |=2，|

  n

  |=3，現有如下命題：
  命題p：|

  m

  -2

  n

  |的值可能為9；
  命題q：“（

  m

  -2

  n

  ）⊥

  m

  ”的充要條件為“cos＜

  m

  ，

  n

  ＞=

  1

  3

  ”；
  則下列命題中，真命題為（　　）

  A．p

  B．p∧q

  C．（￢p）∧q

  D．p∨（￢q）
  組卷：32引用：3難度：0.6

  解析

• 5．已知α∈（0，π），且sinα=

  3

  5

  ，則

  tan

  （

  α

  +

  π

  4

  ）

  =（　　）

  A． - 1 7

  B．7

  C． - 1 7 或-7

  D． 1 7 或7
  組卷：231引用：4難度：0.7

  解析

• 6．函數

  f

  （

  x

  ）

  =

  sin

  2

  x

  +

  x

  3

  e

  |

  x

  |

  在[-2π，2π]上的圖象大致為（　　）

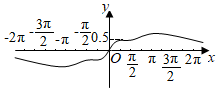
  A．	B．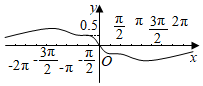
  C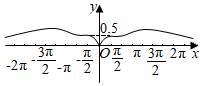．	D．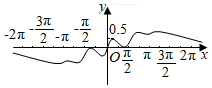
  組卷：107引用：8難度：0.8

  解析

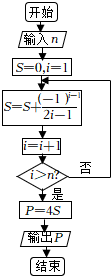• 7．德國數學家萊布尼茲（1646年-1716年）于1674年得到了第一個關于π的級數展開式，該公式于明朝初年傳入我國．在我國科技水平業已落后的情況下，我國數學家、天文學家明安圖（1692年-1765年）為提高我國的數學研究水平，從乾隆初年（1736年）開始，歷時近30年，證明了包括這個公式在內的三個公式，同時求得了展開三角函數和反三角函數的6個新級數公式，著有《割圓密率捷法》一書，為我國用級數計算π開創了先河．如圖所示的程序框圖可以用萊布尼茲“關于π的級數展開式”計算π的近似值（其中P表示π的近似值），若輸入n=10，則輸出的結果是（　　）

  A． P = 4 （ 1 - 1 3 + 1 5 - 1 7 + … + 1 17 ）

  B． P = 4 （ 1 - 1 3 + 1 5 - 1 7 + …- 1 19 ）

  C． P = 4 （ 1 - 1 3 + 1 5 - 1 7 + … + 1 21 ）

  D． P = 4 （ 1 - 1 3 + 1 5 - 1 7 + …- 1 21 ）
  組卷：49引用：12難度：0.7

  解析

（二）選考題：共10分，考生從22、23題中任選一題作答，如果多做，則按所做的第一題計分.作答時用2B鉛筆在答題卡上將所選題目對應的題號涂黑.[選修4--4：坐標系與參數方程]

• 22．在直角坐標系xOy中，曲線C的參數方程

  x = 2 3 cosβ

  y = 2 sinβ

  （β為參數）．直線l的參數方程

  x = 3 + tcosα

  y = 1 + tsinα

  （t為參數）．
  （Ⅰ）求曲線C在直角坐標系中的普通方程；
  （Ⅱ）以坐標原點O為極點，x軸的正半軸為極軸建立極坐標系，當曲線C截直線l所得線段的中點極坐標為

  （

  2

  ，

  π

  6

  ）

  時，求直線l的傾斜角．
  組卷：319引用：4難度：0.5

  解析

[選修4-5：不等式選講]（10分）

• 23．已知函數f（x）=|x-3|-2|x|．
  （1）求不等式f（x）≥2的解集；
  （2）若f（x）的最大值為m,a,b,c為正數且a+b+c=m,求證：a²+b²+c²≥3．
  組卷：72引用：6難度：0.7

  解析