當前位置：試卷中心 > 試卷詳情

2022-2023學年遼寧省大連市高二（上）期末數學試卷

發布：2024/12/14 4:30:1

一、單項選擇題：本大題共8小題，每題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

1．若直線l的方向向量是
e
=
（
1
，
3
）
，則直線l的傾斜角為（　　）
A．
π
6
B．
π
3
C．
2
π
3
D．
5
π
6
組卷：260引用：6難度：0.8
解析
2．已知空間向量
a
=
（
-
1
，
2
，
x
）
，
b
=
（
3
，-
6
，-
3
）
，且
a
∥
b
，則x=（　　）
A．9 B．-1 C．1 D．-9
組卷：101引用：2難度：0.7
解析
3．已知橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的左、右焦點分別為F₁，F₂，上、下頂點分別為A，B，若四邊形AF₁BF₂為正方形，則橢圓C的離心率為（　　）
A．
1
2
B．
2
2
C．
3
2
D．
2
組卷：348引用：3難度：0.7
解析
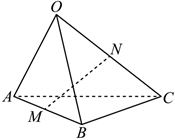4．已知三棱錐O-ABC中，點M，N分別為AB，OC的中點，且
OA
=
a
，
OB
=
b
，
OC
=
c
，則
NM
=（　　）
A．
1
2
（
b
+
c
-
a
）
B．
1
2
（
a
+
b
+
c
）
C．
1
2
（
a
-
b
+
c
）
D．
1
2
（
a
+
b
-
c
）
組卷：190引用：7難度：0.7
解析
5．已知圓M的圓心在直線y=2x（x＞0）上，若圓M與x軸交于A，B兩點，圓M與y軸交于C，D兩點，則（　　）
A．|AB|＜|CD| B．|AB|=|CD| C．|AB|＞|CD| D．|AB|≥|CD|
組卷：80引用：2難度：0.5
解析
6．已知一個動圓P與兩圓
C
1
：
（
x
+
2
）
2
+
y
2
=
1
和
C
2
：
（
x
-
2
）
2
+
y
2
=
4
都外切，則動圓P圓心的軌跡方程為（　　）
A．
4
x
2
-
4
y
2
15
=
1
（
x
＜
0
）
B．
4
x
2
-
4
y
2
15
=
1
C．
4
x
2
9
-
4
y
2
7
=
1
（
x
＜
0
）
D．
4
x
2
9
-
4
y
2
7
=
1
組卷：107引用：1難度：0.7
解析
7．若四棱柱ABCD-A₁B₁C₁D₁的所有棱長均為2，且∠A₁AB=∠A₁AD=∠BAD=60°，則A₁到平面ABCD的距離為（　　）
A．
6
3
B．
6
2
C．
2
6
3
D．
3
組卷：101引用：2難度：0.5
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分.解答應寫出文字說明，證明過程或演算步驟．

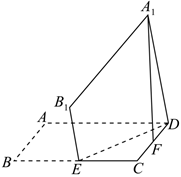21．如圖，在邊長為2的正方形ABCD中，E，F分別為BC，CD的中點．以DE為折痕將四邊形ABED折起，使A，B分別到達A₁，B₁，且平面A₁B₁ED⊥平面CDE．設P為線段CE上一點，且A₁，B₁，P，F四點共面．
（1）證明：B₁E∥平面A₁DF；
（2）求CP的長；
（3）求平面A₁B₁PF與平面CDE所成角的余弦值．
組卷：144引用：2難度：0.4
解析
22．已知橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的左、右焦點分別為F₁，F₂，且|F₁F₂|=2．過F₂的一條斜率存在且不為零的直線交C于M，N兩點，△MNF₁的周長為
4
2
．
（1）求C的方程；
（2）設M關于x軸的對稱點為P，直線PN交x軸于點Q，過Q作C的一條切線，切點為T，證明：∠TF₂P=∠TF₂N．
組卷：115引用：2難度：0.5
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A． 4 x 2 - 4 y 2 15 = 1 （ x ＜ 0 ）	B． 4 x 2 - 4 y 2 15 = 1
C． 4 x 2 9 - 4 y 2 7 = 1 （ x ＜ 0 ）	D． 4 x 2 9 - 4 y 2 7 = 1

2022-2023學年遼寧省大連市高二（上）期末數學試卷

一、單項選擇題：本大題共8小題，每題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

1．若直線l的方向向量是e=（1，3），則直線l的傾斜角為（ ）

2．已知空間向量a=（-1，2，x），b=（3，-6，-3），且a∥b，則x=（ ）

3．已知橢圓C：x2a2+y2b2=1（a＞b＞0）的左、右焦點分別為F1，F2，上、下頂點分別為A，B，若四邊形AF1BF2為正方形，則橢圓C的離心率為（ ）

4．已知三棱錐O-ABC中，點M，N分別為AB，OC的中點，且OA=a，OB=b，OC=c，則NM=（ ）

5．已知圓M的圓心在直線y=2x（x＞0）上，若圓M與x軸交于A，B兩點，圓M與y軸交于C，D兩點，則（ ）

6．已知一個動圓P與兩圓C1：（x+2）2+y2=1和C2：（x-2）2+y2=4都外切，則動圓P圓心的軌跡方程為（ ）

7．若四棱柱ABCD-A1B1C1D1的所有棱長均為2，且∠A1AB=∠A1AD=∠BAD=60°，則A1到平面ABCD的距離為（ ）

四、解答題：本題共6小題，共70分.解答應寫出文字說明，證明過程或演算步驟．

1．若直線l的方向向量是
e
=
（
1
，
3
）
，則直線l的傾斜角為（　　）

2．已知空間向量
a
=
（
-
1
，
2
，
x
）
，
b
=
（
3
，-
6
，-
3
）
，且
a
∥
b
，則x=（　　）

3．已知橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的左、右焦點分別為F₁，F₂，上、下頂點分別為A，B，若四邊形AF₁BF₂為正方形，則橢圓C的離心率為（　　）

4．已知三棱錐O-ABC中，點M，N分別為AB，OC的中點，且
OA
=
a
，
OB
=
b
，
OC
=
c
，則
NM
=（　　）

5．已知圓M的圓心在直線y=2x（x＞0）上，若圓M與x軸交于A，B兩點，圓M與y軸交于C，D兩點，則（　　）

6．已知一個動圓P與兩圓
C
1
：
（
x
+
2
）
2
+
y
2
=
1
和
C
2
：
（
x
-
2
）
2
+
y
2
=
4
都外切，則動圓P圓心的軌跡方程為（　　）

7．若四棱柱ABCD-A₁B₁C₁D₁的所有棱長均為2，且∠A₁AB=∠A₁AD=∠BAD=60°，則A₁到平面ABCD的距離為（　　）