2022-2023學年四川大學附中高一(下)月考數學試卷(3月份)
發布:2024/7/6 8:0:9
一、選擇題(共8小題,每小題5分,共40分。在每個小題給出的四個選項中,只有一項是符合題目要求的.)
-
1.
=( )cosπ12A. 6+24B. 6-24C. -6+24D. -6-24組卷:201引用:7難度:0.7 -
2.函數f(x)=sinx+1的零點是( )
A. π2+2kπ(k∈Z)B. 3π2+2kπ(k∈Z)C. π2+kπ(k∈Z)D.kπ(k∈Z) 組卷:140引用:4難度:0.7 -
3.下列四個函數中,周期為π的是( )
A. y=sinx2B.y=tan2x C.y=|sin2x| D.y=5+cos2x 組卷:160引用:4難度:0.8 -
4.用五點法作函數
的圖象時,所取的“五點”是( )f(x)=sin(2x-π3)A.( ,0),(π6,1),(5π12,0),(2π3,-1),(11π12,0)7π6B.( ,0),(π6,1),(5π12,0),(2π3,-1),(11π12,0)11π6C.( ,0),(π6,1),(5π12,1),(2π3,-1),(11π12,0)7π6D.( ,0),(π6,0),(5π12,0),(2π3,-1),(11π12,0)7π6組卷:144引用:2難度:0.8 -
5.已知M,N,P,Q是平面內四個互不相同的點,
為不共線向量,a,b,MN=a+5b,NP=-2(a-4b),則( )PQ=3(a-b)A.M,N,P三點共線 B.M,N,Q三點共線 C.M,P,Q三點共線 D.N,P,Q三點共線 組卷:324引用:5難度:0.7 -
6.已知a=cos
,則有( )9π5,b=sin20π7,c=tan19π3A.a>b>c B.a>c>b C.c>a>b D.c>b>a 組卷:161引用:6難度:0.7 -
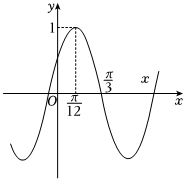 7.已知函數的部分圖象如圖所示,則( )f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<π2)
7.已知函數的部分圖象如圖所示,則( )f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<π2)A.函數 為奇函數f(x+7π12)B.函數f(x)的圖象關于點 對稱(π6,0)C.函數f(x)在區間 上為單調函數[-7π24,π4]D.函數f(x)在區間[0,6π]上有12個零點 組卷:361引用:4難度:0.7
四、解答題(共6小題,17題10分,其余每小題10分,共70分。)
-
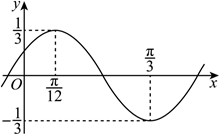 21.已知函數的圖象如圖所示.f(x)=13sin(ωx+φ)(ω>0)
21.已知函數的圖象如圖所示.f(x)=13sin(ωx+φ)(ω>0)
(1)求函數f(x)的對稱中心;
(2)先將函數y=f(x)圖象上所有點的縱坐標伸長到原來的3倍(橫坐標不變),然后將得到的函數圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),最后將所得圖象向左平移個單位后得到函數y=g(x)的圖象.若|g(x)-t|≤1對任意的π3恒成立,求實數t的取值范圍.x∈[-5π12,0]組卷:547引用:11難度:0.5 -
22.已知函數
.f(x)=2sin(2ωx+π6)+1
(1)若,求f(x)的對稱中心;f(x1)≤f(x)≤f(x2),|x1-x2|min=π2
(2)已知0<ω<5,函數f(x)圖象向右平移個單位,得到函數g(x)的圖象,π6是g(x)的一個零點,若函數g(x)在[m,n](m,n∈R且m<n)上恰好有10個零點,求n-m的最小值;x=π3
(3)已知函數,在第(2)問條件下,若對任意h(x)=acos(2x-π6)-2a+3(a>0),存在x1∈[0,π4],使得h(x1)=g(x2)成立,求實數a的取值范圍.x2∈[0,π4]組卷:1281引用:5難度:0.3


