當前位置：試卷中心 > 試卷詳情

2022-2023學年廣東省東莞市東華松山湖高級中學高三（上）月考數學試卷（9月份）

發布：2024/9/27 11:0:2

1．若z=
2
i
1
+
i
，則復數z的虛部是（　　）
A．2i B．i C．2 D．1
組卷：84引用：3難度：0.8
解析
2．已知集合A={x∈N|-1＜x＜lnk}共有8個子集，則實數k的取值范圍為（　　）
A．（0，3] B．（e,e³] C．（e²，e³] D．（e³，e⁴]
組卷：75引用：4難度：0.7
解析
3．已知tanα=-3，則
cos
（
α
+
π
4
）
sinα
+
2
cosα
=（　　）
A．
2
2
5
B．
-
2
2
C．
-
2
5
D．
-
2
組卷：119引用：5難度：0.7
解析
4．若1＜α＜3，-2＜β＜4，則α-|β|的取值范圍是（　　）
A．（-3，1） B．（-3，3） C．（0，3） D．（-3，5）
組卷：1引用：2難度：0.8
解析
5．函數f（x）=4x-lnx的單調遞減區間為（　　）
A．（0，+∞） B．
（
0
，
1
4
）
C．
（
-
∞
，
1
4
）
D．
（
1
4
，
+
∞
）
組卷：25引用：4難度：0.7
解析
6．方程lnx=4-2x的根所在的區間是（　　）
A．（0，1） B．（1，2） C．（2，3） D．（3，4）
組卷：30引用：5難度：0.7
解析
7．設函數
f
（
x
）
=
2
x
x
-
2
在區間[3，4]上的最大值和最小值分別為M，m,則M+m=（　　）
A．4 B．6 C．10 D．24
組卷：901引用：4難度：0.6
解析

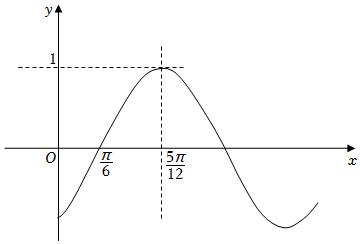21．已知函數f（x）=sin（ωx+φ）（ω＞0，
|
φ
|
＜
π
2
）部分圖象如下圖所示．
（1）求函數f（x）的解析式，并寫出f（x）單調遞增區間；
（2）函數g（x）=4^f（x）-a?2^f（x）+3（a∈R），若對任意
x
∈
[
π
4
，
π
2
]
，都有g（x）≥0恒成立，求實數a取值范圍．
組卷：102引用：3難度：0.5
解析
22．已知函數f（x）=ae^x-ln（x+1）+lna-1．
（1）若a=1，求函數f（x）的單調區間及極值；
（2）若函數f（x）有且僅有兩個零點，求實數a的取值范圍．
組卷：35引用：2難度：0.1
解析