2022-2023學年江西省撫州市崇仁二中九年級（上）第一次月考數學試卷

一、選擇題（共6小題）

• 1．菱形具有而矩形不一定具有的性質是（　　）

  A．對角線互相平分	B．對角線相等
  C．鄰邊互相垂直	D．對角線互相垂直
  組卷：1487引用：16難度：0.8

  解析

• 2．如圖，四邊形ABCD是菱形，頂點A，C的坐標分別是（0，2），（8，2），點D在x軸上，則頂點B的坐標是（　　）

  A．（4，2）

  B．（5，2）

  C．（4，4）

  D．（5，4）
  組卷：944引用：10難度：0.8

  解析

• 3．用配方法解方程x²-4x-1=0時，配方后得到的方程為（　　）

  A．（x+2）2=3

  B．（x+2）2=5

  C．（x-2）2=3

  D．（x-2）2=5
  組卷：362引用：11難度：0.6

  解析

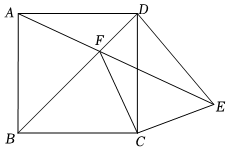• 4．如圖，點E為正方形ABCD外一點，且ED=CD，連接AE，交BD于點F．若∠CDE=38°，則∠BFC的度數為（　　）

  A．71°

  B．72°

  C．81°

  D．82°
  組卷：944引用：7難度：0.5

  解析

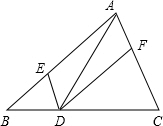• 5．如圖，在△ABC中，點D、E、F分別在邊AB、BC、CA上，且DE∥CA，DF∥BA．下列四種說法，其中正確的有（　　）個
  ①四邊形AEDF是平行四邊形：
  ②如果∠BAC=90°，則四邊形AEDF是矩形：
  ③如果AD平分∠BAC，則四邊形AEDF是菱形：
  ④如果AD⊥BC且AB=AC，則四邊形AEDF是菱形，

  A．1

  B．2

  C．3

  D．4
  組卷：836引用：10難度：0.4

  解析

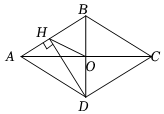• 6．如圖，菱形ABCD的對角線AC、BD相交于點O，過點D作DH⊥AB于點H，連接OH，OH=4，若菱形ABCD的面積為32

  3

  ，則CD的長為（　　）

  A．4

  B．4 3

  C．8

  D．8 3
  組卷：4170引用：23難度：0.2

  解析

二.填空題（共6小題）

• 7．若關于x的一元二次方程x²+2x+m=0的一根為-1，則m的值是

  ．
  組卷：361引用：9難度：0.5

  解析

五.解答題（共2小題）

• 22．如圖，△ABC中，MN∥BD交AC于P，∠ACB、∠ACD的平分線分別交MN于E、F．
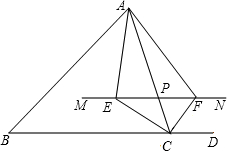
  （1）求證：PE=PF；
  （2）當MN與AC的交點P在什么位置時，四邊形AECF是矩形，說明理由；
  （3）在（2）條件中，當△ABC滿足什么條件時，四邊形AECF是正方形．（不需要證明）
  組卷：2117引用：23難度：0.3

  解析

六.解答題（共1小題）

• 23．探究問題：
  （1）方法感悟：
  如圖1，在正方形ABCD中，點E、F分別為DC、BC邊上的點，且滿足∠EAF=45°，連接EF，求證：DE+BF=EF．
  感悟解題方法，并完成下列填空：
  將△ADE繞點A順時針旋轉90°得到△ABG，此時AD與AB重合，由旋轉可得：
  AB=AD，BG=DE，∠1=∠2，∠ABG=∠D=90°，
  ∴∠ABG+∠ABF=90°+90°=180°，
  因此，點G、B、F在同一條直線上．
  ∵∠EAF=45°，
  ∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°．
  ∵∠1=∠2，∴∠1+∠3=45°．
  即∠GAF=∠

   

  ．
  又　AG=AE，AF=AF，∴△GAF≌

   

  ．
  ∴

   

  =EF，故DE+BF=EF；
  （2）方法遷移：
  如圖2，將Rt△ABC沿斜邊翻折得到△ADC，點E、F分別為DC、BC邊上的點，且∠EAF=

  1

  2

  ∠DAB．試猜想DE、BF、EF之間有何數量關系，并證明你的猜想；
  （3）問題拓展：
  如圖3，在四邊形ABCD中，AB=AD，E、F分別為DC、BC上的點，滿足∠EAF=

  1

  2

  ∠DAB，試猜想當∠B與∠D滿足什么關系時，可使得DE+BF=EF．請直接寫出你的猜想（不必說明理由）．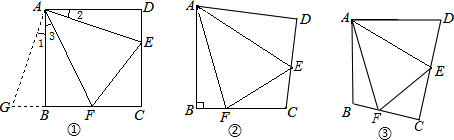
  
  組卷：510引用：7難度：0.1

  解析