2021-2022學(xué)年重慶八中高三（上）周考數(shù)學(xué)試卷（二）

一、選擇題：本大題共8小題，每小題5分，共40分．在每小題給出的四個(gè)備選項(xiàng)中，只有一項(xiàng)是符合題目要求的.

• 1．已知集合A={x|log₂（x+1）＜2}，B={x|2x²-5x-3≤0}，則A∪B=（　　）

  A． { x | - 1 2 ＜ x ≤ 3 }

  B．{x|-1＜x≤3}

  C． { x | - 1 2 ≤ x ＜ 3 }

  D．{x|x≤3}
  組卷：168引用：5難度：0.8

  解析

• 2．用二分法求函數(shù)f（x）=log₂x+a-2x零點(diǎn)的近似值時(shí)，如果確定零點(diǎn)所處的初始區(qū)間為（

  1

  4

  ，

  1

  2

  ），那么a的取值范圍為（　　）

  A．（-∞，2）	B．（ 5 2 ，+∞）
  C．（2， 5 2 ）	D．（-∞，2）∪（ 5 2 ，+∞）
  組卷：231引用：3難度：0.9

  解析

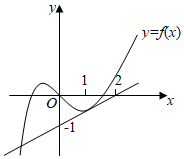• 3．曲線y=f（x）在x=1處的切線如圖所示，則f′（1）-f（1）=（　　）

  A．0

  B．-1

  C．1

  D．- 1 2
  組卷：523引用：12難度：0.8

  解析

• 4．設(shè)復(fù)數(shù)z=（a²-4）+（a-3）i（其中a實(shí)數(shù)，i為虛數(shù)單位），則“a=2”是“z為虛數(shù)”的（　　）

  A．充分非必要條件	B．充要條件
  C．既非充分又非必要條件	D．必要非充分條件
  組卷：5引用：1難度：0.8

  解析

• 5．某市一診考試的數(shù)學(xué)成績(jī)近似地服從正態(tài)分布N（96，5²）．據(jù)此估計(jì)：在全市抽取6名高三學(xué)生的數(shù)學(xué)成績(jī)，恰有2名同學(xué)的成績(jī)超過(guò)96分的概率為（　　）

  A． 1 32

  B． 15 32

  C． 1 64

  D． 15 64
  組卷：6引用：1難度：0.7

  解析

• 6．函數(shù)f（x）的定義域?yàn)镽，f（-1）=3，對(duì)任意x∈R，f′（x）＜3，則f（x）＞3x+6的解集為（　　）

  A．{x|-1＜x＜1}

  B．{x|x＞-1}

  C．{x|x＜-1}

  D．R
  組卷：290引用：3難度：0.8

  解析

• 7．已知log₄a=0.6，9^b=8，c=ln2，則（　　）

  A．c＜b＜a

  B．c＜a＜b

  C．b＜c＜a

  D．a(chǎn)＜c＜b
  組卷：226引用：2難度：0.6

  解析

四、解答題：本題共6小題，共70分。解答應(yīng)寫出文字說(shuō)明、證明過(guò)程或演算步驟.

• 21．已知雙曲線

  C

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的右焦點(diǎn)F與拋物線y²=8x的焦點(diǎn)重合，一條漸近線的傾斜角為30^o．
  （1）求雙曲線C的方程；
  （2）經(jīng)過(guò)點(diǎn)F的直線與雙曲線的右支交于A，B兩點(diǎn)，與y軸交于P點(diǎn)，點(diǎn)P關(guān)于原點(diǎn)的對(duì)稱點(diǎn)為點(diǎn)Q，求△QAB的面積的取值范圍．
  組卷：60引用：3難度：0.4

  解析

• 22．已知函數(shù)f（x）=xlnx-ax²，a∈R．
  （1）若f（x）存在單調(diào)遞增區(qū)間，求a的取值范圍；
  （2）若x₁，x₂為f（x）的兩個(gè)不同極值點(diǎn)，證明：3lnx₁+lnx₂＞-1．
  組卷：195引用：4難度：0.3

  解析