2022-2023學年江蘇省無錫一中高三（上）月考數學試卷（10月份）

一、選擇題：本題共8小題，每小題5分，共40分，在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．若復數z=

  1

  +

  2

  i

  1

  -

  i

  -1，則z在復平面內的對應點位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：22引用：2難度：0.9

  解析

• 2．設集合A={x|m-3＜x＜2m+6}，B={x|log₂x＜2}，若A∪B=A，則實數m的取值范圍是（　　）

  A．?

  B．[-3，-1]

  C．（-1，3）

  D．[-1，3]
  組卷：118引用：8難度：0.7

  解析

• 3．函數f（x）=2（x-x³）e^|x|的圖象大致是（　　）

  A．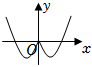

  B．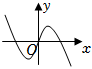

  C．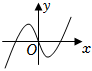

  D．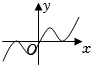
  組卷：110引用：3難度：0.8

  解析

• 4．已知{a_n}為等差數列，S_n為{a_n}的前n項和．若S₁₀＜0，a₃+a₇＞0，則當S_n取最大值時，n的值為（　　）

  A．3

  B．4

  C．5

  D．6
  組卷：569引用：5難度：0.8

  解析

• 5．已知a＞0，b＜0，且a-3b+2ab=0，則3a-b的最小值是（　　）

  A．6

  B．8

  C．12

  D．16
  組卷：190引用：3難度：0.7

  解析

• 6．把一條線段分為兩部分，使其中一部分與全長之比等于另一部分與這部分之比，其比值是一個無理數

  5

  -

  1

  2

  ，由于按此比例設計的造型十分美麗柔和，因此稱為黃金分割，黃金分割不僅僅體現在諸如繪畫、雕塑、音樂、建筑等藝術領域，而且在管理、工程設計等方面也有著不可忽視的作用．在△ABC中，點D為線段BC的黃金分割點（BD＞DC），AB=2，AC=3，∠BAC=60°，則

  AD

  ?

  BC

  =（　　）

  A． 7 5 - 9 2

  B． 9 - 7 5 2

  C． 9 5 - 7 2

  D． 7 - 9 5 2
  組卷：171引用：7難度：0.5

  解析

• 7．已知定義在[0，+∞）上的函數f（x）滿足：對任意的x₁，x₂∈[0，+∞），x₁≠x₂，都有

  f

  （

  x

  2

  ）

  -

  f

  （

  x

  1

  ）

  x

  2

  -

  x

  1

  ＞2，f（1）=2022，則滿足不等式f（x-2022）＞2（x-1012）的x的解集是（　　）

  A．（2022，+∞）

  B．（2023，+∞）

  C．[2022，2023）

  D．[2021，2023）
  組卷：267引用：5難度：0.5

  解析

四、解答題：本題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

• 21．已知函數

  f

  （

  x

  ）

  =

  lnx

  +

  a

  2

  x

  2

  （

  a

  ∈

  R

  ）

  ．
  （1）當a=1時，對于函數G（x）=f（x）-3lnx,存在x₁，x₂∈[1，4]，使得G（x₁）-G（x₂）≥m成立，求滿足條件的最大整數m；（ln2≈0.693）
  （2）設函數

  g

  （

  x

  ）

  =

  2

  3

  x

  3

  ，若f（x）≤g（x）在

  [

  e

  ，

  +

  ∞

  ）

  上恒成立，求實數a的取值范圍．
  組卷：76引用：3難度：0.4

  解析

• 22．設f（x）=ae^x-2x-1，其中a∈R．
  （1）討論f（x）的單調性；
  （2）令F（x）=e^xf（x）+

  5

  4

  a

  （a≠0），若F（x）≤0在R上恒成立，求a的最小值．
  組卷：133引用：8難度：0.3

  解析