2023年浙江省金華市曙光學校高考數(shù)學三模試卷

一、選擇題（本題共8小題，每小題5分共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。）

• 1．全集U={x|x≤9，x∈N^*}，A={1，3，5，6}，B={1，3，7，9}，則B∩?_UA=（　　）

  A．{1，3，7，9}

  B．{1，7，9}

  C．{3，7，9}

  D．{7，9}
  組卷：96引用：3難度：0.7

  解析

• 2．已知復數(shù)z滿足（1+i）z=2，則|z|=（　　）

  A．1

  B． 2

  C．2

  D． 2 2
  組卷：30引用：11難度：0.9

  解析

• 3．函數(shù)

  y

  =

  ln

  （

  cosx

  ）

  ，

  x

  ∈

  （

  -

  π

  2

  ，

  π

  2

  ）

  的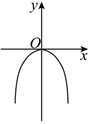圖象大致形如（　　）

  A．

  B．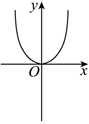

  C．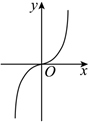

  D．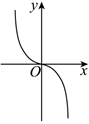
  組卷：70引用：3難度：0.9

  解析

• 4．已知向量

  a

  =

  （

  2

  ，

  1

  ）

  ，

  b

  =

  （

  -

  1

  ，

  1

  ）

  ，向量

  a

  在

  b

  方向上的投影向量為（　　）

  A． 2 2 b

  B． - 2 2 b

  C． 1 2 b

  D． - 1 2 b
  組卷：132引用：4難度：0.8

  解析

• 5．如圖1，位于西安大慈恩寺的大雁塔是我國現(xiàn)存最早、規(guī)模最大的唐代四方樓閣式磚塔，其最高處的塔剎可以近似地看成一個正四棱錐，如圖2，已知正四棱錐P-ABCD的高為4.87m,其側棱與高的夾角為45°，則該正四棱錐的體積約為（　　）（4.87³≈115.5）
  

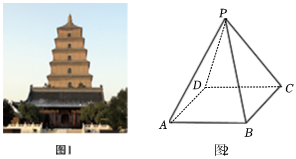
  A．231m3

  B．179m3

  C．154m3

  D．77m3
  組卷：123引用：4難度：0.7

  解析

• 6．已知F₁，F(xiàn)₂分別為雙曲線：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的左，右焦點，點P為雙曲線漸近線上一點，若PF₁⊥PF₂，

  tan

  ∠

  P

  F

  1

  F

  2

  =

  1

  4

  ，則雙曲線的離心率為（　　）

  A． 17 8

  B． 17 15

  C． 15 8

  D． 8 5
  組卷：204引用：4難度：0.6

  解析

• 7．已知函數(shù)f（x）=acosωx（a≠0，ω＞0），若將函數(shù)y=f（x）的圖象向左平移

  π

  6

  ω

  個單位長度后得到函數(shù)y=g（x）的圖象，若關于x的方程g（x）=0在

  [

  0

  ，

  7

  π

  12

  ]

  上有且僅有兩個不相等的實根，則實數(shù)ω的取值范圍是（　　）

  A． [ 10 7 ， 24 7 ）

  B． [ 16 7 ， 4 ）

  C． [ 10 7 ， 4 ）

  D． [ 16 7 ， 24 7 ）
  組卷：228引用：7難度：0.6

  解析

四、解答題（本大題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。）

• 21．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （a＞b＞0）的左、右焦點分別為F₁，F(xiàn)₂，P（x₀，y₀）是橢圓C上異于左、右頂點的動點，△PF₁F₂的周長為6，橢圓C的離心率為

  1

  2

  ．
  （1）求橢圓C的標準方程；
  （2）若圓E與△PF₁F₂的三邊都相切，判斷是否存在定點M，N，使|EM|+|EN|為定值．若存在，求出點M，N的坐標；若不存在，請說明理由．
  組卷：137引用：6難度：0.3

  解析

• 22．已知函數(shù)f（x）=e^x+xcosx.
  （1）求函數(shù)f（x）在x=0處的切線方程；
  （2）判斷函數(shù)f（x）在[0，+∞）上的單調(diào)性，并說明理由；
  （3）對任意的x≥0，e^x+xsinx+cosx≥ax+2，求實數(shù)a的取值范圍．
  組卷：162引用：2難度：0.6

  解析