2022-2023學年浙江大學附中玉泉校區高二（上）期末數學試卷

一、單項選擇題（本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．直線

  y

  =

  3

  x

  +

  1

  的傾斜角為（　　）

  A． π 6

  B． π 3

  C． 5 π 6

  D． 2 π 3
  組卷：183引用：4難度：0.9

  解析

• 2．已知數列{a_n}的前n項和S_n=2ⁿ-2，則該數列的通項公式為（　　）

  A． a n = 2 n	B． a n = 2 n - 1
  C． a n = 0 ， n = 1 2 n ， n ≥ 2	D． a n = 0 ， n = 1 2 n - 1 ， n ≥ 2
  組卷：289引用：2難度：0.8

  解析

• 3．已知數列{a_n}為等差數列，S_n是其前n項和，若a₄=3，a₉=5，則S₁₂=（　　）

  A．96

  B．72

  C．48

  D．60
  組卷：293引用：3難度：0.7

  解析

• 4．已知直線（m+1）x+3y+1=0與直線4x+my+1=0平行，則m的值為（　　）

  A．3

  B．-4

  C．3或-4

  D．3或4
  組卷：501引用：8難度：0.8

  解析

• 5．雙曲線

  x

  2

  9

  -

  y

  2

  16

  =

  1

  的左頂點到其漸近線的距離為（　　）

  A．2

  B． 9 5

  C． 12 5

  D．3
  組卷：138引用：4難度：0.7

  解析

• 6．點P是拋物線y²=4x上一動點，則點P到點A（0，-1）的距離與點P到直線x=-2的距離和的最小值是（　　）

  A． 5

  B． 2

  C． 2 - 1

  D． 2 + 1
  組卷：349引用：6難度：0.6

  解析

• 7．已知橢圓E：

  x

  2

  20

  +

  y

  2

  16

  =

  1

  與雙曲線C：

  x

  2

  a

  2

  -

  y

  2

  =

  1

  （

  a

  ＞

  0

  ）

  有共同的焦點，則雙曲線C的漸近線方程為（　　）

  A． y =± 3 x

  B． y =± 3 3 x

  C． y =± 5 x

  D． y =± 5 5 x
  組卷：169引用：4難度：0.7

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

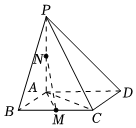• 21．如下圖，在四棱錐P-ABCD中，PA⊥平面ABCD，底面ABCD是菱形，AB=2，∠ABC=60°，點M，N分別為BC，PA的中點．
  （1）證明：MN∥平面PCD；
  （2）若直線AC與平面PBC所成角的正弦值為

  21

  7

  ，求平面PAC與平面PCD夾角的余弦值．
  組卷：124引用：2難度：0.5

  解析

• 22．已知橢圓

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的左、右焦點分別是F₁，F₂，且離心率為

  1

  2

  ，點M為橢圓上的動點，△F₁MF₂面積最大值為

  3

  ．
  （1）求橢圓C的標準方程；
  （2）M，N是橢圓C上的動點，且直線經過定點

  （

  0

  ，

  1

  2

  ）

  ，問在y軸上是否存在定點Q，使得∠MQO=∠NQO？若存在，請求出定點Q；若不存在，請說明理由．
  組卷：128引用：2難度：0.4

  解析