2022-2023學年上海市楊浦區控江中學高二（下）月考數學試卷（3月份）

一、填空題（本大題共有12題，滿分54分，第1～6題每題4分，第7～12題每題5分）

• 1．半徑為1的球的表面積是

  ．
  組卷：348引用：12難度：0.9

  解析

• 2．雙曲線x²-y²=1的兩條漸近線的夾角大小為

  ．
  組卷：75引用：3難度：0.7

  解析

• 3．在正方體ABCD-A₁B₁C₁D₁中，直線BA₁與平面A₁B₁CD所成的角是

  ．
  組卷：9引用：3難度：0.7

  解析

• 4．從1，2，3，4，5，6，7，8，9這9個數中任取4個不同的數，其和為偶數，則不同的取法有

  種？
  組卷：19引用：1難度：0.7

  解析

• 5．已知圓錐的底面半徑為1，其側面展開圖為一個半圓，則該圓錐的體積為

  ．
  組卷：173引用：6難度：0.7

  解析

• 6．兩個實習生每人加工一個零件，加工為一等品的概率分別為

  2

  3

  和

  3

  4

  ，兩個零件是否加工為一等品相互獨立，則這兩個零件中恰有一個一等品的概率為

  ．
  組卷：216引用：12難度：0.7

  解析

• 7．已知雙曲線方程為

  x

  2

  9

  -

  y

  2

  16

  =

  1

  ，點P是該雙曲線上的點，F₁、F₂分別是它的左、右焦點，若|PF₁|?|PF₂|=32，則∠F₁PF₂的大小為

  ．
  組卷：68引用：1難度：0.5

  解析

三、解答題（本大題共有5題，滿分76分）解答下列各題必須在答題紙的相應位置寫出必要的步驟．

• 20．我國古代數學名著《九章算術》中記載：“芻（chú）甍（méng）者，下有袤有廣，而上有袤無廣．芻，草也．甍，窟蓋也．”翻譯為“底面有長有寬為矩形，頂部只有長沒有寬為一條棱．芻甍的字面意思為茅草屋頂．”
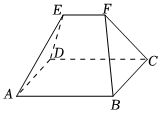
  現有一個“芻甍”如圖所示，四邊形ABCD為正方形，四邊形ABFE、CDEF為兩個全等的等腰梯形，EF∥AB，AB=4，EF=2，

  EA

  =

  ED

  =

  FB

  =

  FC

  =

  17

  ．
  （1）設過點F且與直線EF垂直的平面為平面α，且平面α與直線AB、CD分別交于P、Q兩點，求△FPQ的周長；
  （2）求四面體ABDE的體積；
  （3）點N在線段AD上且滿足

  AN

  AD

  =

  1

  3

  ．試問：在線段CF上是否存在點M，使NF∥平面BDM？若存在，求出

  CM

  CF

  的值；若不存在，請說明理由．
  組卷：65引用：2難度：0.5

  解析

• 21．已知橢圓Γ的方程為

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （常數a＞b＞0），點A為橢圓短軸的上端點，點P是橢圓Γ上異于點A的一個動點．若動點P到定點A的距離的最大值僅在P點為短軸得另一頂點時取到，則稱此橢圓為“圓橢圓”，已知b=2．
  （1）若a=5，判斷橢圓Γ是否為“圓橢圓”；
  （2）若橢圓Γ是“圓橢圓”，求a的取值范圍；
  （3）已知橢圓Γ是“圓橢圓”，且a取最大值，點P關于原點O的對稱點為點Q（點Q也異于點A），且直線AP、AQ分別與x軸交于M、N兩點．試問以線段MN為直徑的圓是否過定點？證明你的結論．
  組卷：63引用：3難度：0.4

  解析