2022-2023學年北京市順義區牛欄山一中高一(下)月考數學試卷(6月份)
發布:2024/5/26 8:0:9
一、選擇題(本大題共10小題,每小題4分,共40分,四個選項中只有一是符合題目)
-
1.已知正四棱錐的底面邊長為2,高為3,則它的體積為( )
A.2 B.4 C.6 D.12 組卷:468引用:4難度:0.8 -
2.復數z=i(1+i)(i是虛數單位)在復平面內所對應點的坐標為( )
A.(1,1) B.(-1,-1) C.(1,-1) D.(-1,1) 組卷:17引用:9難度:0.9 -
3.將函數f(x)=sin2x的圖象向右平移φ個單位長度后得到函數
的圖象,則φ的最小值是( )f(x)=sin(2x-π3)A. π6B. π3C. 2π3D. 5π6組卷:315引用:3難度:0.8 -
4.已知直線m和平面α,β,則下列四個命題中正確的是( )
A.若α⊥β,m?β,則m⊥α B.若m∥α,m∥β,則α∥β C.若α∥β,m∥α,則m∥β D.若α∥β,m⊥α,則m⊥β 組卷:152引用:10難度:0.7 -
5.在△ABC中,
,則∠A=( )3asinB=3bcosAA. 5π6B. 2π3C. π3D. π6組卷:682引用:4難度:0.8 -
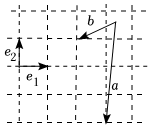 6.向量,a,b,e在正方形網格中的位置如圖所示,若e2a=λ-b+μe1(λ,μ∈R),則e2=( )λμ
6.向量,a,b,e在正方形網格中的位置如圖所示,若e2a=λ-b+μe1(λ,μ∈R),則e2=( )λμA.3 B. 13C.-3 D. -13組卷:392引用:8難度:0.7
三、解答題(本大題共6小題,共85分,解答應寫出文字說明過程或演算步驟.)
-
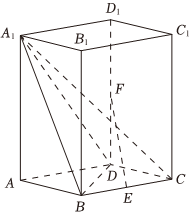 19.如圖,在直棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,AB=2,∠BAD=60°,AA1=a,E,F分別是棱BC,DD1的中點.
19.如圖,在直棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,AB=2,∠BAD=60°,AA1=a,E,F分別是棱BC,DD1的中點.
(Ⅰ)求證:BD⊥A1C;
(Ⅱ)求證:EF∥平面A1BD;
(Ⅲ)若平面A1BC⊥平面A1DC,求a的值.組卷:329引用:1難度:0.4 -
20.若點(x0,y0)在函數f(x)的圖象上,且滿足y0?f(y0)≥0,則稱x0是f(x)的ξ點.函數f(x)的所有ξ點構成的集合稱為f(x)的ξ集.
(Ⅰ)判斷是否是函數f(x)=tanx的ξ點,并說明理由;2π3
(Ⅱ)若函數f(x)=sin(πx),求f(x)的ξ集;
(Ⅲ)若定義域為R的連續函數f(x)的ξ集D是實數集的真子集,求證:{x|f(x)=0}≠?.組卷:8引用:1難度:0.5


