2021-2022學(xué)年浙江省嘉興市高二(下)期末數(shù)學(xué)試卷
發(fā)布:2025/1/7 12:30:2
一、選擇題(本大題共8小題,每小題5分,共40分.在每小題給出的四個(gè)選項(xiàng)中,只有一項(xiàng)是符合題目要求的)
-
1.已知集合A={x|x2-3x<0},B={x|x-2>0},則A∩B=( )
A.(0,2) B.(2,3) C.(-3,2) D.(0,+∞) 組卷:102引用:1難度:0.7 -
2.已知直線l、m和平面α.若m?α,l?α,則“l(fā)∥m”是“l(fā)∥α”的( )
A.充分不必要條件 B.必要不充分條件 C.充分必要條件 D.既不充分也不必要條件 組卷:254引用:3難度:0.7 -
3.已知平面向量
,a=(1,0),若b=(1,2),則實(shí)數(shù)λ=( )(a+λb)⊥aA.-1 B.-2 C. -12D.1 組卷:186引用:7難度:0.7 -
4.函數(shù)
的部分圖象可能是( )f(x)=x3+x3x+3-xA. 
B. 
C. 
D.  組卷:270引用:7難度:0.9
組卷:270引用:7難度:0.9 -
5.將A,B,C,D,E五個(gè)字母排成一排,且A,E均不排在兩端,則不同的排法共有( )
A.108種 B.72種 C.36種 D.18種 組卷:126引用:3難度:0.8 -
6.設(shè)函數(shù)
若函數(shù)y=f(x)+a在R上有4個(gè)不同的零點(diǎn),則實(shí)數(shù)a的取值范圍是( )f(x)=ax2+ax+1,x≤0,|lnx|,x>0,A. (-43,+∞)B.(-∞,0) C.[-1,0) D. (-43,-1]組卷:326引用:2難度:0.5 -
7.下列說(shuō)法錯(cuò)誤的是( )
A.當(dāng)P(A)>0時(shí),當(dāng)且僅當(dāng)事件A與B相互獨(dú)立時(shí),有P(B|A)=P(B) B.一元回歸模型分析中,對(duì)一組給定的樣本數(shù)據(jù)(xi,yi)(i=1,2,…,n),當(dāng)樣本數(shù)據(jù)的線性相關(guān)程度越強(qiáng)時(shí),樣本相關(guān)系數(shù)r的值越接近于1 C.利用最小二乘法得到的經(jīng)驗(yàn)回歸直線 必經(jīng)過(guò)樣本數(shù)據(jù)的中心?y=?bx+?a(x,y)D.由χ2進(jìn)行分類(lèi)變量獨(dú)立性檢驗(yàn)時(shí),應(yīng)用不同的小概率值α?xí)茢喑霾煌慕Y(jié)論 組卷:21引用:1難度:0.8
四、解答題:本大題共6小題,共70分.解答應(yīng)寫(xiě)出文字說(shuō)明、證明過(guò)程或演算步驟.
-
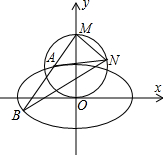 21.如圖,已知橢圓C1:+x2a2=1(a>b>0)經(jīng)過(guò)點(diǎn)(y2b2,2),離心率為22,點(diǎn)M(0,2b),以O(shè)M為直徑作圓C2,過(guò)點(diǎn)M作相互垂直的兩條直線,分別交橢圓C1與圓C2于點(diǎn)A、B和點(diǎn)N.32
21.如圖,已知橢圓C1:+x2a2=1(a>b>0)經(jīng)過(guò)點(diǎn)(y2b2,2),離心率為22,點(diǎn)M(0,2b),以O(shè)M為直徑作圓C2,過(guò)點(diǎn)M作相互垂直的兩條直線,分別交橢圓C1與圓C2于點(diǎn)A、B和點(diǎn)N.32
(1)求橢圓C1的標(biāo)準(zhǔn)方程;
(2)當(dāng)△NAB的面積最大時(shí),求直線AB的方程.組卷:88引用:1難度:0.3 -
22.已知函數(shù)
.f(x)=lnx-a2x2+1(a∈R)
(Ⅰ)討論函數(shù)f(x)的單調(diào)性;
(Ⅱ)設(shè)函數(shù)f(x)有兩個(gè)不同的零點(diǎn)x1,x2(x1<x2),
(ⅰ)求證;0<a<e(e=2.71828?為自然對(duì)數(shù)的底數(shù));
(ⅱ)若x1,x2滿足,求a的最大值.|lnx1-lnx2|≥ln22組卷:168引用:2難度:0.3


