2020學年人教新版九年級上學期《22.1.2 二次函數y=ax2的圖象和性質》中考真題套卷（1）

一、選擇題（共10小題）

• 1．一次函數y=ax+c（a≠0）與二次函數y=ax²+bx+c（a≠0）在同一平面直角坐標系中的圖象可能是（　　）

  A．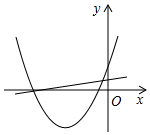

  B．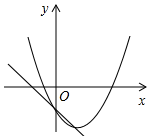

  C．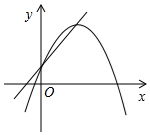

  D．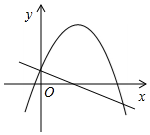
  組卷：13333引用：31難度：0.9

  解析

• 2．關于拋物線y=x²-2x+1，下列說法錯誤的是（　　）

  A．開口向上

  B．與x軸有兩個重合的交點

  C．對稱軸是直線x=1

  D．當x＞1時，y隨x的增大而減小
  組卷：7956引用：23難度：0.9

  解析

• 3．下列函數中，y總隨x的增大而減小的是（　　）

  A．y=4x

  B．y=-4x

  C．y=x-4

  D．y=x2
  組卷：2783引用：29難度：0.8

  解析

• 4．在同一平面直角坐標系中，函數y=ax+b與y=ax²-bx的圖象可能是（　　）

  A．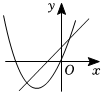

  B．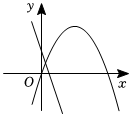

  C．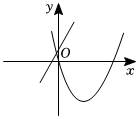

  D．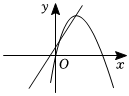
  組卷：10383引用：63難度：0.7

  解析

• 5．如圖，函數y=ax²-2x+1和y=ax-a（a是常數，且a≠0）在同一平面直角坐標系的圖象可能是（　　）

  A．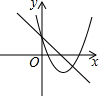

  B．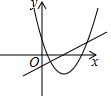

  C．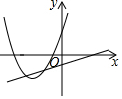

  D．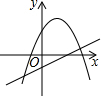
  組卷：10530引用：98難度：0.7

  解析

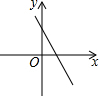• 6．已知一次函數y=

  b

  a

  x+c的圖象如圖，則二次函數y=ax²+bx+c在平面直角坐標系中的圖象可能是（　　）

  A．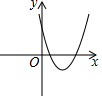

  B．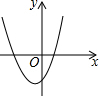

  C．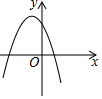

  D．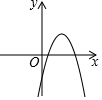
  組卷：7433引用：46難度：0.7

  解析

三、解答題（共5小題）

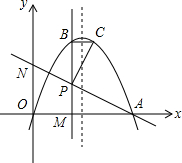• 19．拋物線y=-x²+4ax+b（a＞0）與x軸相交于O、A兩點（其中O為坐標原點），過點P（2，2a）作直線PM⊥x軸于點M，交拋物線于點B，點B關于拋物線對稱軸的對稱點為C（其中B、C不重合），連接AP交y軸于點N，連接BC和PC．
  （1）a=

  3

  2

  時，求拋物線的解析式和BC的長；
  （2）如圖a＞1時，若AP⊥PC，求a的值；
  （3）是否存在實數a,使

  AP

  PN

  =

  1

  2

  ？若存在，求出a的值，如不存在，請說明理由．
  組卷：1009引用：10難度：0.3

  解析

• 20．我們規定：若

  m

  =（a,b），

  n

  =（c,d），則

  m

  ?

  n

  =ac+bd.如

  m

  =（1，2），

  n

  =（3，5），則

  m

  ?

  n

  =1×3+2×5=13．
  （1）已知

  m

  =（2，4），

  n

  =（2，-3），求

  m

  ?

  n

  ；
  （2）已知

  m

  =（x-a,1），

  n

  =（x-a,x+1），求y=

  m

  ?

  n

  ，問y=

  m

  ?

  n

  的函數圖象與一次函數y=x-1的圖象是否相交，請說明理由．
  組卷：1354引用：16難度：0.1

  解析