當前位置：試卷中心 > 試卷詳情

2022-2023學年廣東省河源市高三（上）期末數學試卷

發布：2024/4/20 14:35:0

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．已知集合A={x||x|＜2}，B={x|y=ln（a-2x）}，且A∩B={x|-2＜x＜1}，則a=（　　）
A．-4 B．-2 C．2 D．4
組卷：54引用：1難度：0.8
解析
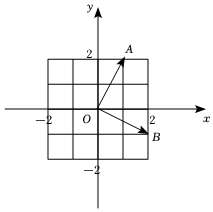2．如圖，在復平面內，復數z₁，z₂對應的向量分別是
OA
，
OB
，且復數
z
3
=
3
+
z
1
z
2
，若復數z₃，z₄在復平面內的對應點關于虛軸對稱，則z₄=（　　）
A．3-i B．3+i C．-3-i D．-3+i
組卷：59引用：1難度：0.7
解析
3．已知平面向量
a
，
b
滿足
a
=
（
1
，-
1
）
，
|
b
|
=
1
，
|
a
+
2
b
|
=
2
，則向量
a
與向量
a
+
2
b
的夾角為（　　）
A．
π
6
B．
π
4
C．
π
3
D．
π
2
組卷：518引用：2難度：0.7
解析
4．如圖所示，一款網紅冰激凌可近似地看作是圓錐和半球的組合體，將圓錐外的包裝紙展開發現，它是一張半徑為6的半圓形紙片，則這個冰激凌的體積為（　　）
A．27π B．
18
π
+
9
3
π
C．
36
π
+
9
3
π
D．54π
組卷：116引用：1難度：0.6
解析
5．已知角α的頂點為坐標原點，始邊與x軸的非負半軸重合，終邊過點P（sin138°，cos138°），則tan（α+18°）=（　　）
A．
3
B．
3
3
C．
-
3
D．
-
3
3
組卷：127引用：1難度：0.8
解析
6．在數列{a_n}中，a₁=1，a_n＞0，且na_n+1²-a_na_n+1-（n+1）a_n²=0，則a₂₀的值為（　　）
A．18 B．19 C．20 D．21
組卷：198引用：3難度：0.6
解析
7．（x-2y-1）⁵的展開式中含x²y²的項的系數為（　　）
A．-120 B．60 C．-60 D．30
組卷：520引用：5難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

21．已知橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的四個頂點圍成的四邊形面積為
4
2
，周長為
4
6
，一雙曲線E的頂點是該橢圓的焦點，焦點是該橢圓長軸上的頂點．
（1）求橢圓C和雙曲線E的標準方程；
（2）A，B，D是雙曲線E上不同的三點，且B，D兩點關于y軸對稱，△ABD的外接圓經過原點O．求證：直線AB與圓x²+y²=1相切．
組卷：73引用：1難度：0.6
解析
22．已知函數f（x）=e^x-ax,g（x）=ln（x+2）-a,其中e為自然對數的底數，a∈R．
（1）當a＞0時，函數f（x）有極小值f（1），求a；
（2）證明：f'（x）＞g（x）恒成立；
（3）證明：
ln
2
+
（
ln
3
2
）
2
+
（
ln
4
3
）
3
+
…
+
（
ln
n
+
1
n
）
n
＜
e
e
-
1
．
組卷：667引用：4難度：0.6
解析