2022-2023學年河南省南陽市方城縣高一（下）期末數學試卷

一．單選題（每題5分共40分）

• 1．計算

  4

  （

  1

  +

  i

  ）

  6

  的結果是（　　）

  A． i 4

  B． - i 4

  C． i 2

  D． - i 2
  組卷：35引用：2難度：0.7

  解析

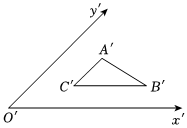• 2．如圖所示是利用斜二測畫法畫出的水平放置的△ABC的直觀圖，已知A′C′∥y′軸，B′C′∥x′軸且2A′C′=B′C′=2，則△ABC的周長為（　　）

  A． 4 + 2 2

  B． 2 + 2 2

  C． 2 + 2 3

  D． 4 + 3
  組卷：135引用：5難度：0.7

  解析

• 3．sin210°cos120°的值為（　　）

  A． 1 4

  B．- 3 4

  C．- 3 2

  D． 3 4
  組卷：254引用：11難度：0.9

  解析

• 4．已知

  sin

  （

  6

  π

  5

  +

  α

  ）

  =

  3

  3

  ，則

  cos

  （

  3

  π

  5

  -

  2

  α

  ）

  =（　　）

  A． - 2 3

  B． - 1 3

  C． 2 3

  D． 1 3
  組卷：239引用：3難度：0.7

  解析

• 5．已知向量

  a

  =

  （

  λ

  +

  1

  ，

  4

  ）

  ，

  b

  =

  （

  3

  ，

  λ

  ）

  ，若

  a

  與

  b

  反向，則向量

  c

  =

  （

  1

  ，

  2

  ）

  在向量

  a

  -

  b

  上的投影向量為（　　）

  A．（6，-8）

  B．（-6，8）

  C． （ 3 5 ，- 4 5 ）

  D． （ - 3 5 ， 4 5 ）
  組卷：72引用：3難度：0.7

  解析

• 6．下列表述中正確的是（　　）

  A．若直線a∥平面α，直線b⊥a,則b⊥α

  B．若直線a?平面α，直線b?α，且 a ⊥ b ，則a⊥α

  C．若平面α內有三個不共線的點到平面β的距離相等，則α∥β

  D．若平面α，β滿足α⊥β，α⊥γ，β∩γ=l,則l⊥α
  組卷：52引用：2難度：0.8

  解析

• 7．已知函數

  f

  （

  x

  ）

  =

  2

  3

  co

  s

  2

  x

  +

  （

  cosx

  -

  sinx

  ）

  2

  -

  3

  ，則（　　）

  A．f（x）的最小正周期為 π 2

  B．f（x）的一條對稱軸為 x = π 6

  C．f（x）在 [ π 6 ， 2 π 3 ] 上單調遞減

  D．f（x）的圖象關于點 （ π 6 ， 1 ） 中心對稱
  組卷：67引用：2難度：0.6

  解析

四．解答題（共70分）

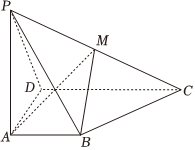• 21．如圖，在四棱錐P-ABCD中，AB∥CD，AB⊥平面PAD，PA=AD=DC=2AB=4，PD=2

  7

  ，M是PC的中點．
  （1）證明：BM∥面PAD；
  （2）證明：平面ABM⊥平面PCD；
  （3）求三棱錐M-PAB的體積．
  組卷：302引用：4難度：0.5

  解析

• 22．已知函數y=f（x），若存在實數m、k（m≠0），使得對于定義域內的任意實數x,均有m?f（x）=f（x+k）+f（x-k）成立，則稱函數f（x）為“可平衡”函數；有序數對（m,k）稱為函數f（x）的“平衡”數對．
  （1）若f（x）=x²，求函數f（x）的“平衡”數對；
  （2）若m=1，判斷f（x）=sinx是否為“可平衡”函數，并說明理由；
  （3）若m₁、m₂∈R，且

  （

  m

  1

  ，

  π

  2

  ）

  、

  （

  m

  2

  ，

  π

  4

  ）

  均為函數

  f

  （

  x

  ）

  =

  co

  s

  2

  x

  （

  0

  ＜

  x

  ≤

  π

  4

  ）

  的“平衡”數對，求

  m

  2

  1

  +

  m

  2

  2

  的取值范圍．
  組卷：55引用：14難度：0.6

  解析