2023-2024學年遼寧省沈陽120中高二（上）期初數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中,只有一項是符合題目要求的。

• 1．已知

  {

  a

  ，

  b

  ，

  c

  }

  是空間的一組基底，則可以與向量

  p

  =

  a

  +

  b

  ，

  q

  =

  a

  -

  b

  構成基底的向量（　　）

  A． a

  B． b

  C． a + b

  D． a + 2 c
  組卷：147引用：2難度：0.8

  解析

• 2．下列函數中，最小正周期為2π的奇函數是（　　）

  A．y=tanx	B．y=cosx
  C．y=sin（x+3π）	D．y=sin2x
  組卷：106引用：3難度：0.8

  解析

• 3．設m,n是兩條不同的直線，α，β是兩個不同的平面，則下列結論中正確的是（　　）

  A．若m∥n,n∥α，則m∥α	B．若m∥α，n∥α，則m∥n
  C．若m∥n,m∥α，n∥β，則α∥β	D．若m⊥α，n⊥β，α⊥β，則m⊥n
  組卷：93引用：6難度：0.7

  解析

• 4．函數f（x）=

  sin

  （

  πx

  ）

  x

  2

  的圖象大致為（　　）

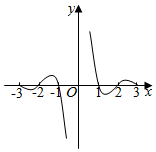
  A．	B．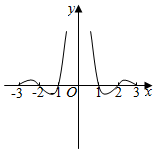
  C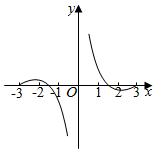．	D．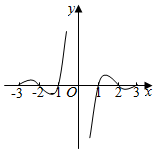
  組卷：102引用：6難度：0.8

  解析

• 5．羽毛球運動是一項全民喜愛的體育運動，標準的羽毛球由16根羽毛固定在球托上，測得每根羽毛在球托之外的長為8cm,球托之外由羽毛圍成的部分可看成一個圓臺的側面，測得頂部所圍成圓的直徑是6cm,底部所圍成圓的直徑是2cm,據此可估算球托之外羽毛球所在曲面的展開圖的圓心角為（　　）

  A． 2 π 3

  B． 3 π 4

  C． π 2

  D． π 3
  組卷：97引用：3難度：0.7

  解析

• 6．已知函數

  f

  （

  x

  ）

  =

  xsin

  （

  ωx

  +

  π

  4

  ）

  ，

  ?

  x

  1

  ，

  x

  2

  ∈

  （

  π

  2

  ，

  5

  π

  6

  ）

  ，且x₁＜x₂，都有x₂f（x₁）-x₁f（x₂）＞0，則ω的取值范圍可能是（　　）

  A． [ 1 2 ， 3 2 ]

  B． [ 1 2 ， 5 4 ]

  C． [ 3 2 ， 9 4 ]

  D． [ 0 ， 1 2 ]
  組卷：224引用：4難度：0.5

  解析

• 7．已知四棱錐P-ABCD的底面ABCD是邊長為2的正方形，且∠PAB=90°．若四棱錐P-ABCD的五個頂點在同一球面上，已知棱PA最大值為

  2

  5

  ，則四棱錐P-ABCD的外接球體積為（　　）

  A．24π

  B． 8 6 π

  C．28π

  D． 28 7 3 π
  組卷：156引用：3難度：0.5

  解析

四、解答題：本題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

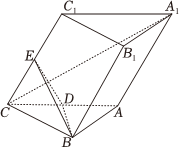• 21．如圖，在三棱柱 ABC-A₁B₁C₁ 中，底面是邊長為2的等邊三角形，CC₁=2，D，E分別是線段AC，CC₁的中點，C₁在平面ABC內的射影為D．
  （1）求證：A₁C⊥平面BDE；
  （2）若點F為線段 B₁C₁上的動點（不包括端點），求銳二面角F-BD-E的余弦值的取值范圍．
  組卷：182引用：8難度：0.5

  解析

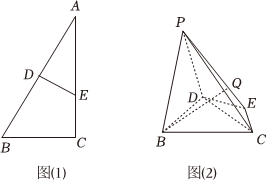• 22．如圖（1）所示，在△ABC中，AB=4

  3

  ，BC=2

  3

  ，∠B=60°，DE垂直平分AB．現將△ADE沿DE折起，使得二面角A-DE-B大小為60°，得到如圖（2）所示的空間幾何體（折疊后點A記作點P）
  （1）求點D到面PEC的距離；
  （2）求四棱錐P-BCED外接球的體積；
  （3）點Q為一動點，滿足

  PQ

  =

  λ

  PE

  （0＜λ＜1），當直線BQ與平面PEC所成角最大時，試確定點Q的位置．
  組卷：64引用：2難度：0.5

  解析