2014年五年級數學思維訓練：構造認證一

一、解答題（共30小題，滿分0分）

• 1．如圖，用1×2和1×3兩種規格的小長方形地板磚鋪滿的地面，至少需要地板磚多少塊？
  
  組卷：19引用：3難度：0.9

  解析

• 2．國際象棋的皇后可以控制她所在的橫線、豎線和斜線，如圖中一個皇后（圖中五角星）就把整個3×3的棋盤控制了．為了控制一個4×4的棋盤至少要放幾個皇后？
  組卷：24引用：3難度：0.7

  解析

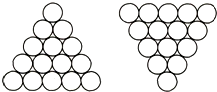• 3．如圖中的左圖為15枚硬幣組成的三角形，如果僅移動5枚硬幣，要把這些硬幣變成右圖的形式，應該怎樣移動？請在圖中表示出移動的方法．
  組卷：50引用：3難度：0.9

  解析

• 4．把100個橘子分裝在6個籃子里，使得每個籃子里裝的橘子數都含有數字6，應該如何裝？
  組卷：38引用：3難度：0.9

  解析

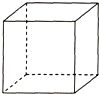• 5．把正方體的所有棱染成白色或者紅色，要求每個面上至少要有一條棱是白色的．請問：最少有多少條棱是白色的？
  組卷：32引用：3難度：0.7

  解析

• 6．請在9，8，…，3，2，1的相鄰兩個數之間填入“+”或者“-”（不能改變數的順序），使得結果是1．能否使得結果是0呢？
  
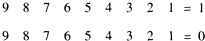  組卷：53引用：1難度：0.7

  解析

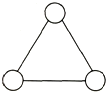• 7．如圖，能否在三角形的三個頂點各填一個自然數，使得每條邊的兩個頂點上的數之和都是奇數？如果能，請寫出一種填法；如果不能，請說明理由．
  組卷：34引用：3難度：0.7

  解析

• 8．四位同學進行了一次乒乓球單打比賽，當比賽進行了若干場后，體育老師問他們分別比賽了多少場．這四位同學回答分別比了1、2、3、3場．老師說：“你們肯定有人記錯了．”請問：老師是怎么知道的呢？
  組卷：24引用：3難度：0.5

  解析

• 9．有四個算式：口+口=口，口-口=口，口×口=口，口÷口=口，如果每一個算式中都至少有1個偶數和1個奇數，那么12個數中一共有多少個偶數？如果沒有前面的限制，這12個數中最少有多少個偶數？最多有多少個偶數？
  組卷：29引用：3難度：0.7

  解析

• 10．有14個孩子，依次給他們編號為1，2，3，…，14．能否把他們分成三組，使得每組都有一個孩子的編號是該組其它孩子的編號之和．
  組卷：46引用：3難度：0.7

  解析

一、解答題（共30小題，滿分0分）

• 29．旅店現在有9個單人間，10名旅客可能入住．這10名旅客每次有9個人同時入住，管理員想事先給每個人配一些鑰匙，使得無論是哪9個人入住，總能正好入住這9個房間，而且不用找別人借鑰匙，請問：最少需要多少把鑰匙？
  組卷：38引用：2難度：0.1

  解析

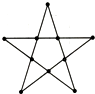• 30．如圖，在五角星圖案中共有10個節點（用黑色實心圓點表示），以這些節點為頂點的三角形共有10個．現在將自然數1至10分別填在10個節點上，將每個三角形中三個頂點處所標數的和稱為此三角形的“特征值”．請問：
  （1）是否存在一種填數方法，使得每個三角形的特征值均為偶數；
  （2）是否存在一種填數方法，使得每個三角形的特征值都能被3整除．能則舉出例子，不能請說明理由．
  組卷：45引用：3難度：0.1

  解析