2022-2023學年云南省怒江新城新時代中學高一（下）期中數學試卷

一、單選題（本大題共8小題，共40.0分）

• 1．已知集合M={-2，1，2，3}，N={-2，2}，下列結論成立的是（　　）

  A．M?N

  B．M∩N=?

  C．M∪N=M

  D．?MN={1}
  組卷：183引用：10難度：0.9

  解析

• 2．已知a、b∈R，則“a²＞b²”是“|a|＞|b|”的（　　）

  A．充分非必要條件	B．必要非充分條件
  C．充要條件	D．既非充分又非必要條件
  組卷：2566引用：8難度：0.9

  解析

• 3．命題“?x∈R，x²-2x+2≤0”的否定是（　　）

  A．?x∈R，x2-2x+2≥0	B．?x∈R，x2-2x+2＞0
  C．?x∈R，x2-2x+2≤0	D．?x∈R，x2-2x+2＞0
  組卷：133引用：39難度：0.7

  解析

• 4．若x＞0，則x+

  9

  x

  +2有（　　）

  A．最小值6

  B．最小值8

  C．最大值4

  D．最大值3
  組卷：151引用：3難度：0.9

  解析

• 5．設a=0.6²，b=2^0.6，c=log₂0.6，則a,b,c的大小關系為（　　）

  A．a＞b＞c

  B．a＞c＞b

  C．b＞a＞c

  D．c＞a＞b
  組卷：151引用：6難度：0.7

  解析

• 6．設函數

  f

  （

  x

  ）

  =

  log 2 （ 1 - x ） ， x ＜ 0

  2 x - 1 ， x ≥ 0

  ，則f（-3）+f（log₂3）=（　　）

  A．4

  B．5

  C． 5 2

  D． 7 2
  組卷：130引用：2難度：0.8

  解析

• 7．函數g（x）=2^x+5x的零點x₀所在的一個區間是（　　）

  A．（-2，-1）

  B．（-1，0）

  C．（0，1）

  D．（1，2）
  組卷：105引用：4難度：0.9

  解析

四、解答題（本大題共6小題，共70.0分）

• 21．已知函數f（x）=

  1

  2

  sin（2x-

  π

  3

  ）（x∈R）．
  （1）求f（x）的最小正周期及在區間[0，π]內單調遞增區間；
  （2）求f（x）在區間[-

  π

  4

  ，

  π

  4

  ]上的最大值和最小值．
  組卷：552引用：3難度：0.7

  解析

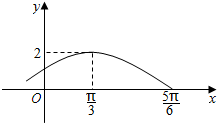• 22．設函數f（x）=Asin（ωx+φ）（A＞0，ω＞0，-

  π

  2

  ＜φ＜

  π

  2

  ，x∈R）的部分圖象如圖所示．
  （1）求函數y=f（x）的解析式；
  （2）當x∈[-

  π

  2

  ，

  π

  2

  ]時，求f（x）的取值范圍．
  組卷：1451引用：4難度：0.5

  解析