2013-2014學(xué)年浙江省杭州市蕭山中學(xué)高一（下）暑假數(shù)學(xué)作業(yè)（理科班）（5）

一、選擇題

• 1．下列命題中不正確的是（　　）

  A．存在這樣的α和β的值，使得cos（α+β）=cosαcosβ+sinαsinβ

  B．不存在無窮多個α和β的值，使得cos（α+β）=cosαcosβ+sinαsinβ

  C．對于任意的α和β，都有cos（α+β）=cosαcosβ-sinαsinβ

  D．不存在這樣的α和β值，使得cos（α+β）≠cosαcosβ-sinαsinβ
  組卷：42引用：5難度：0.7

  解析

• 2．已知全集為R，集合A={x|（

  1

  2

  ）^x≤1}，B={x|x²-6x+8≤0}，則A∩（?_RB）=（　　）

  A．{x|x≤0}	B．{x|2≤x≤4}
  C．{x|0≤x＜2或x＞4}	D．{x|0＜x≤2或x≥4}
  組卷：922引用：72難度：0.9

  解析

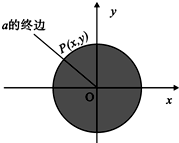• 3．如圖，設(shè)α是一個任意角，它的終邊與單位圓交于點P（x,y），我們把

  1

  x

  叫做α的正割，記作secα；把

  1

  y

  叫做α的余割，記作cscα．則sec

  2

  π

  3

  +csc

  2

  π

  3

  =（　　）

  A．- 3

  B． 3

  C．- 3 3

  D． 3 3
  組卷：28引用：4難度：0.9

  解析

• 4．已知等比數(shù)列{a_n}中，a₁＞0，a₃a₇=16，則a₅=（　　）

  A．±4

  B．4

  C．-4

  D．不能確定
  組卷：12引用：3難度：0.9

  解析

• 5．函數(shù)y=sin（3x+

  π

  3

  ）?cos（x-

  π

  6

  ）+cos（3x+

  π

  3

  ）?cos（x+

  π

  3

  ）的一條對稱軸是（　　）

  A．x= π 6

  B．x= π 4

  C．x=- π 6

  D．x= π 2
  組卷：38引用：3難度：0.9

  解析

• 6．給定數(shù)列{x_n}，x₁=1，且

  x

  n

  +

  1

  =

  3

  x

  n

  +

  1

  3

  -

  x

  n

  ，則x₁+x₂+…x₂₀₁₁=（　　）

  A．1

  B．-1

  C．2+ 3

  D．-2+ 3
  組卷：41引用：2難度：0.9

  解析

三、解答題

• 19．已知公差為d（d＞1）的等差數(shù)列{a_n}和公比為q（q＞1）的等比數(shù)列{b_n}，滿足集合{a₃，a₄，a₅}∪{b₃，b₄，b₅}={1，2，3，4，5}
  （1）求通項a_n，b_n；
  （2）求數(shù)列{a_nb_n}的前n項和S_n；
  （3）若恰有4個正整數(shù)n使不等式

  2

  a

  n

  +

  p

  a

  n

  ≤

  b

  n

  +

  1

  +

  p

  +

  8

  b

  n

  成立，求正整數(shù)p的值．
  組卷：105引用：5難度：0.3

  解析

• 20．已知定義在R上的單調(diào)函數(shù)f（x），存在實數(shù)x₀，使得對于任意實數(shù)x₁，x₂總有f（x₀x₁+x₀x₂）=f（x₀）+f（x₁）+f（x₂）恒成立
  （1）求x₀的值；
  （2）若f（x₀）=1，且對任意正整數(shù)n,有a_n=

  1

  f

  （

  n

  ）

  ，

  b

  n

  =

  f

  （

  1

  2

  n

  ）

  +

  1

  ，記S_n=a₁a₂+a₂a₃+…+a_na_n+1，T_n=b₁b₂+b₂b₃+…+b_nb_n+1，求S_n和T_n；
  （3）若不等式a_n+1+a_n+2+…+a_2n＞

  4

  35

  [

  lo

  g

  1

  2

  （

  x

  +

  1

  ）

  -

  lo

  g

  1

  2

  （

  9

  x

  2

  -

  1

  ）

  +

  1

  ]

  對任意不小于2的正整數(shù)n都成立，求x的取值范圍．
  組卷：24引用：3難度：0.5

  解析