2022-2023學(xué)年山東省威海市文登區(qū)九年級（上）期末數(shù)學(xué)試卷（五四學(xué)制）

一、選擇題（本大題共10小題，各小題3分，共30分．下列各題所給出的四個選項中，只有一個是正確的，每小題選對相3分，選錯、不選或多選，均不得分．）

• 1．若只增大物體與投影面之間的距離，則其正投影（　　）

  A．變大

  B．變小

  C．不變

  D．無法確定
  組卷：301引用：3難度：0.8

  解析

• 2．某小組做“當(dāng)試驗次數(shù)很大時，用頻率估計概率”的試驗時，統(tǒng)計了某一結(jié)果出現(xiàn)的頻率，表格如下，則不符合這一結(jié)果的試驗最有可能是（　　）
  

  次數(shù)	200	400	600	800	1000
  頻率	0.21	0.29	0.30	0.32	0.33

  A．三張撲克牌，牌面分別是5，7，8，背面朝上洗勻后，隨機抽出一張牌面是5

  B．?dāng)S一枚質(zhì)地均勻的骰子，向上的面的點數(shù)為3的倍數(shù)

  C．在玩石頭、剪刀、布的游戲中，小明隨機出的是剪刀

  D．?dāng)S一枚一元的硬幣，正面朝上
  組卷：191引用：3難度：0.6

  解析

• 3．在邊長相等的小正方形組成的網(wǎng)格中，點A，B，C都在格點上，那么cos∠BAC的值為（　　）

  A． 5 5

  B． 2 5 5

  C． 1 2

  D． 1 3
  組卷：397引用：5難度：0.8

  解析

• 4．若點（-3，y₁）、（-1，y₂）、（2，y₃）均在反比例函數(shù)

  y

  =

  1

  x

  上，則y₁，y₂，y₃的大小關(guān)系是（　　）

  A．y1＞y2＞y3

  B．y1＜y2＜y3

  C．y2＜y1＜y3

  D．y1＞y3＞y2
  組卷：53引用：1難度：0.6

  解析

• 5．將某拋物線向左平移3個單位，再向上平移2個單位，得到拋物線y=2（x+3）²+4，則原拋物線的解析式為（　　）

  A．y=2x2+2	B．y=2（x+6）2+2
  C．y=2x2+6	D．y=（x+6）2+6
  組卷：127引用：1難度：0.7

  解析

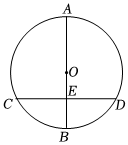• 6．如圖，AB為⊙O的直徑，弦CD⊥AB于點E，若AE=CD=8，則⊙O的半徑為（　　）

  A．3

  B．4

  C． 9 2

  D．5
  組卷：344引用：2難度：0.6

  解析

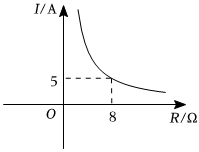• 7．某蓄電池的電壓為定值，使用蓄電池時，電流I（單位：A）與電阻R（單位：Ω）是反比例函數(shù)關(guān)系，其圖象如圖所示．若以此蓄電池為電源的用電器，其限制電流不超過10A，那么用電器可變電阻R應(yīng)控制的范圍是（　　）

  A．R＞4

  B．R≥4

  C．R＜4

  D．R≤4
  組卷：117引用：1難度：0.7

  解析

• 8．若二次函數(shù)y=x²-2x-k與x軸沒有交點，則二次函數(shù)y=x²+（k+1）x+k的圖象的頂點在（　　）

  A．第四象限

  B．第三象限

  C．第二象限

  D．第一象限
  組卷：622引用：6難度：0.6

  解析

三、解答題（本大題共8小題，共72分．）

• 23．如圖，二次函數(shù)y=ax²+bx+c的圖象與x軸交于A，B兩點，與y軸交于點C（0，3），頂點D的坐標(biāo)為（-1，4）．分別連接AD，CD，AC，BC．
  
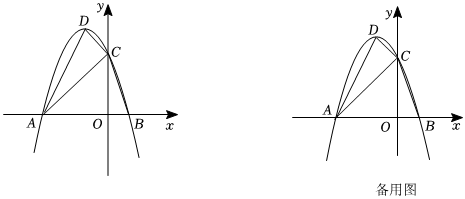
  （1）求二次函數(shù)的表達式；
  （2）求證：∠CAD=∠BCO．
  組卷：113引用：1難度：0.4

  解析

• 24．【初識模型】如圖1，在△ABC中，AB=AC，∠BAC=90°．點D為BC邊上一點，以AD為邊作△ADE，使∠DAE=90°，AE=AD，連接CE，則CE與BD的數(shù)量關(guān)系是

  ；
  【構(gòu)建模型】如圖2，△ABC內(nèi)接于⊙O，BC為⊙O的直徑，AB=AC，點E為弧AC上一點，連接AE，BE，CE．若CE=3，BE=9，求AE的長；
  【運用模型】如圖3，等邊△ABC內(nèi)接于⊙O，點E為弧AC上一點，連接AE，BE，CE．若CE=6，BE=10，求AE的長．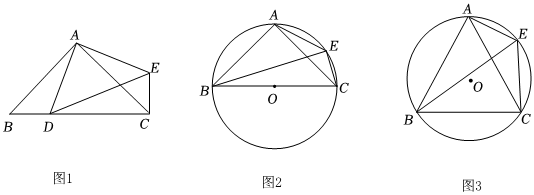
  
  組卷：167引用：1難度：0.3

  解析