2015-2016學年貴州省遵義市仁懷市周林高中高一（下）開學數學試卷

一.選擇題（本大題共12小題，每小題5分，滿分60分．在每小題給出的四個選項中，只有一項是符合題目要求的．）

• 1．已知集合M={1，2，3}，N={2，3，4}，M∩N為（　　）

  A．{2，3}

  B．{1，2，3，4}

  C．{1，2，3}

  D．{1，4}
  組卷：22引用：9難度：0.9

  解析

• 2．冪函數y=x^a（α是常數）的圖象（　　）

  A．一定經過點（0，0）	B．一定經過點（1，1）
  C．一定經過點（-1，1）	D．一定經過點（1，-1）
  組卷：944引用：22難度：0.9

  解析

• 3．已知點P（tanα，cosα）在第三象限，則角α的終邊在（　　）

  A．第四象限

  B．第三象限

  C．第二象限

  D．第一象限
  組卷：307引用：51難度：0.7

  解析

• 4．已知函數f（x）是定義在[a-1，2a]上的偶函數，則a=（　　）

  A． 1 3

  B． 1 2

  C．1

  D．0
  組卷：23引用：1難度：0.9

  解析

• 5．函數f（x）=2^x+3x的零點所在的一個區間是（　　）

  A．（-2，-1）

  B．（-1，0）

  C．（0，1）

  D．（1，2）
  組卷：1174引用：92難度：0.9

  解析

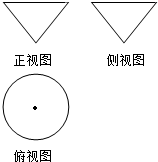• 6．如圖所示是某一容器的三視圖，現向容器中勻速注水，容器中水面的高度h隨時間t變化的可能圖象是（　　）

  A．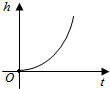

  B．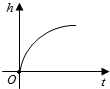

  C．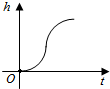

  D．
  組卷：1249引用：69難度：0.9

  解析

• 7．下列四組函數中，表示同一函數的是（　　）

  A．f（x）=|x|，g（x）= x 2

  B．f（x）=lgx2，g（x）=2lgx

  C．f（x）= x 2 - 1 x - 1 ，g（x）=x+1

  D．f（x）= x + 1 ? x - 1 ，g（x）= x 2 - 1
  組卷：1626引用：29難度：0.9

  解析

三.解答題（本大題共6小題，共70分．解答應寫出文字說明和演算過程．）

• 21．已知函數f（x）=Asin（ωx+φ），x∈R（其中

  A

  ＞

  0

  ，

  ω

  ＞

  0

  ，

  0

  ＜

  φ

  ＜

  π

  2

  ）的圖象與x軸的交點中，相鄰兩個交點之間的距離為

  π

  2

  ，且圖象上一個最低點為

  M

  （

  2

  π

  3

  ，-

  2

  ）

  ．
  （Ⅰ）求f（x）的解析式；
  （Ⅱ）當

  x

  ∈

  [

  π

  12

  ，

  π

  2

  ]

  ，求f（x）的值域．
  組卷：1920引用：94難度：0.7

  解析

• 22．設函數y=f（x）是定義域在R，并且滿足f（x+y）=f（x）+f（y），f（

  1

  3

  ）=1，且當x＞0時，f（x）＞0．
  （1）求f（0）的值；
  （2）判斷函數的奇偶性；
  （3）如果f（x）+f（2+x）＜2，求x的取值范圍．
  組卷：245引用：15難度：0.3

  解析