2020-2021學年上海交大附中高三(下)開學數學試卷
發布:2024/10/26 12:30:2
一、填空題.
-
1.計算:
=.limn→∞(2n-3)2n2+3n+1組卷:45引用:1難度:0.7 -
2.方程log2(x-3)+log2(x+4)=3的解為.
組卷:231引用:1難度:0.8 -
3.動點M到點(-1,0)的距離等于M到直線x=1的距離,則點M的軌跡方程為.
組卷:33引用:1難度:0.7 -
4.方程x2-6x+a=0的一個根為x=3+i,其中i為虛數單位,則實數a的值為.
組卷:116引用:1難度:0.8 -
 5.如圖,ABC-DEF是各棱長均為2的正三棱柱,則直線BF與平面ABED所成角的大小為 .(結果用反三角函數表示).組卷:72引用:1難度:0.5
5.如圖,ABC-DEF是各棱長均為2的正三棱柱,則直線BF與平面ABED所成角的大小為 .(結果用反三角函數表示).組卷:72引用:1難度:0.5 -
 6.如圖為某比賽獎杯的三視圖,獎杯的上部是一個球,獎杯的下部是一個圓柱,若獎杯上、下兩部分的體積相等,則上部球的表面積與下部圓柱的側面積之比為.組卷:39引用:2難度:0.6
6.如圖為某比賽獎杯的三視圖,獎杯的上部是一個球,獎杯的下部是一個圓柱,若獎杯上、下兩部分的體積相等,則上部球的表面積與下部圓柱的側面積之比為.組卷:39引用:2難度:0.6 -
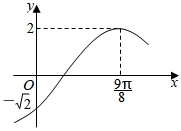 7.如圖為函數的局部圖象,則f(x)的解析式為 .f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤π2)組卷:155引用:1難度:0.6
7.如圖為函數的局部圖象,則f(x)的解析式為 .f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤π2)組卷:155引用:1難度:0.6
三、解答題
-
20.在平面直角坐標系xOy中,已知E(-2,0),F(2,0),A(-1,0),動點P滿足|PE|-|PF|=2,動點P的軌跡記為Γ.
(1)求曲線Γ的方程;
(2)若點Q也在曲線Γ上,且,求△APQ的面積;FP=-3FQ
(3)是否存在常數λ,使得對動點P恒有∠PFA=λ∠PAE成立?請給出你的結論和理由.組卷:90引用:2難度:0.6 -
21.已知集合A?R,若xi∈A(i=1,2,…,n)且x1>x2>…>xn(n≥2,n∈N*),則稱x=x1-x2+x3+…+(-1)n+1xn為集合生成的一個“交錯數”,所有“交錯數”組成的集合B稱為集合A生成的交錯集
(1)寫出集合A={2,5,7,9}生成的交錯集;
(2)若集合A={x|x=3n,n∈N*},求證:集合A的交錯數各不相同;
(3)無窮數列{an}的前n項和為Sn,且對任意n∈N*都有Sn=2an-1.記A={x|x=an,n∈N*},判斷集合A生成的交錯集B與正整數集N*的關系,并說明理由.組卷:58引用:1難度:0.3


