2022-2023學(xué)年黑龍江省大慶市鐵人中學(xué)高二（下）期末數(shù)學(xué)試卷

一、選擇題（1-8單選題，9-12多選題，部分選對(duì)得3分，全部選對(duì)得5分，共60分）

• 1．已知復(fù)數(shù)z滿足z+3=4

  z

  +5i,則在復(fù)平面內(nèi)復(fù)數(shù)z對(duì)應(yīng)的點(diǎn)在（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：346引用：8難度：0.8

  解析

• 2．為了了解高一、高二、高三的身體狀況，現(xiàn)用分層抽樣的方法抽出一個(gè)容量為1200的樣本，三個(gè)年級(jí)學(xué)生數(shù)之比依次為k：5：3，已知高一年級(jí)共抽取了240人，則高三年級(jí)抽取的人數(shù)為（　　）

  A．240

  B．300

  C．360

  D．400
  組卷：61引用：5難度：0.9

  解析

• 3．已知15個(gè)不同數(shù)據(jù)的第25百分位數(shù)是9．則下列說法正確的是（　　）

  A．這15個(gè)數(shù)據(jù)中一定有4個(gè)數(shù)小于9

  B．把這15個(gè)數(shù)據(jù)從小到大排列后，9是第4個(gè)數(shù)據(jù)

  C．把這15個(gè)數(shù)據(jù)從小到大排列后，9是第4個(gè)數(shù)據(jù)和第5個(gè)數(shù)據(jù)的平均數(shù)

  D．把這15個(gè)數(shù)據(jù)從小到大排列后，9是第3個(gè)數(shù)據(jù)和第4個(gè)數(shù)據(jù)的平均數(shù)
  組卷：97引用：3難度：0.7

  解析

• 4．已知一個(gè)圓錐的底面半徑為6，其體積為30π，則該圓錐的側(cè)面積為（　　）

  A．30π

  B．32π

  C．37π

  D．39π
  組卷：108引用：3難度：0.7

  解析

• 5．已知平面向量

  a

  ，

  b

  滿足

  a

  =（-1，2），|

  b

  |=

  10

  ，|

  a

  -

  b

  |=

  5

  ，則

  a

  與

  b

  的夾角為（　　）

  A． π 6

  B． π 4

  C． π 3

  D． π 12
  組卷：131引用：5難度：0.9

  解析

• 6．若球的最大截面圓面積擴(kuò)大為原來的2倍，則球體積擴(kuò)大為原來的（　　）

  A．8倍

  B．4倍

  C． 2 2 倍

  D．2倍
  組卷：13引用：2難度：0.7

  解析

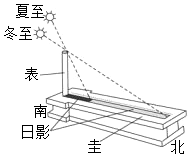• 7．圭表（圭是南北方向水平放置測(cè)定表影長度的刻板，表是與圭垂直的桿）是中國古代用來確定節(jié)令的儀器，利用正午時(shí)太陽照在表上，表在圭上的影長來確定節(jié)令．已知冬至和夏至正午時(shí)，太陽光線與地面所成角分別為α，β，表影長之差為l,那么表高為（　　）

  A． l （ tanα - tanβ ） tanαtanβ	B． ltanαtanβ tanα - tanβ
  C． l （ tanβ - tanα ） tanβtanα	D． ltanβtanα tanβ - tanα
  組卷：98引用：4難度：0.6

  解析

三、解答題（17題10分，18-22題每題12分，共70分）

• 21．在△ABC中，角A，B，C所對(duì)的邊分別為a,b,c,

  m

  =

  （

  cos

  B

  ，

  1

  ）

  ，

  n

  =

  （

  cos

  C

  ，

  3

  sin

  A

  -

  cos

  A

  ）

  ，且

  m

  ∥

  n

  
  （1）求角B的大小；
  （2）若

  b

  =

  3

  ，求a+2c的最大值．
  組卷：347引用：7難度：0.5

  解析

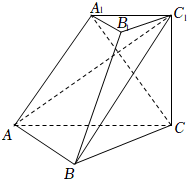• 22．在三棱臺(tái)ABC-A₁B₁C₁中，AC=2，AB=

  3

  2

  ，∠BAC=60°，A₁C₁=1，CC₁=

  2

  ，AC⊥CC₁，側(cè)面ACC₁A₁⊥平面ABC₁．
  （Ⅰ）求證：A₁C⊥平面ABC₁；
  （Ⅱ）求證：△ABC₁是直角三角形；
  （Ⅲ）求直線AA₁與平面ABC所成角的正弦值．
  組卷：266引用：3難度：0.6

  解析