當前位置：試卷中心 > 試卷詳情

2021-2022學年江蘇省南通市如皋市高一（下）期初數學試卷

發布：2024/12/1 6:30:1

一、單項選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．已知集合A={x|x²-2x-8＜0}，B={x|x＞0}，則A∩B=（　　）
A．{x|x＞2} B．{x|0＜x＜2} C．{x|0＜x＜4} D．{x|2＜x＜4}
組卷：117引用：3難度：0.8
解析
2．已知函數f（x）是奇函數，當x≥0時，f（x）=100^x-1，則
f
（
lg
1
2
）
=（　　）
A．1 B．-1 C．3 D．-3
組卷：149引用：4難度：0.8
解析
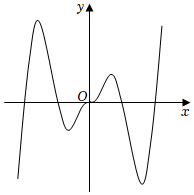3．已知函數f（x）的部分圖象如圖所示，則f（x）的解析式可能為（　　）
A．f（x）=x²cosx B．f（x）=x+x³
C．f（x）=|x|sinx D．f（x）=x²+cosx
組卷：209引用：9難度：0.7
解析
4．將函數
f
（
x
）
=
sin
（
2
x
+
π
3
）
的圖象向左平移m（m＞0）個單位后得到的圖象關于y軸對稱，則正數m的最小值是（　　）
A．
π
12
B．
π
3
C．
5
π
12
D．
5
π
6
組卷：232引用：3難度：0.6
解析
5．德國數學家狄利克雷（1805～1859）在1837年時提出：“如果對于x的每一個值，y總有一個完全確定的值與之對應，那么y是x的函數．”這個定義較清楚地說明了函數的內涵．只要有一個法則，使得取值范圍中的每一個x,有一個確定的y和它對應就行了，不管這個法則是用公式還是用圖象、表格等形式表示，例如狄利克雷函數D（x），即：當自變量取有理數時，函數值為1；當自變量取無理數時，函數值為0．
以下關于狄利克雷函數D（x）的性質：①
D
（
2
）
=
0
；②D（x）的值域為{0，1}；③D（x）為奇函數；④D（x-1）=D（x），其中表述正確的個數是（　　）
A．1 B．2 C．3 D．4
組卷：40引用：4難度：0.8
解析
6．已知
a
=
lo
g
1
2
3
，
b
=
2
sin
2
3
，c=2^-0.1，則（　　）
A．a＜c＜b B．c＜a＜b C．a＜b＜c D．b＜c＜a
組卷：124引用：8難度：0.8
解析
7．已知角θ的終邊經過點（2a+1，a-2），且
cosθ
=
3
5
，則實數的a值是（　　）
A．-2 B．
2
11
C．-2或
2
11
D．1
組卷：358引用：3難度：0.8
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分.請在答題卡指定區域內作答，解答時應寫出文字說明、證明過程或演算步驟.

21．已知函數
f
（
x
）
=
lo
g
2
（
x
2
-
ax
+
a
+
3
）
．
（1）若f（x）的定義域為R，求a的取值范圍；
（2）若f（x）≥1對x∈[2，3]恒成立，求a的取值范圍．
組卷：136引用：7難度：0.5
解析
22．已知函數f（x）的定義域為（-1，1），且滿足：對任意x,y∈（-1，1），都有
f
（
x
）
+
f
（
y
）
=
f
（
x
+
y
1
+
xy
）
．
（1）求證：函數f（x）為奇函數；
（2）若當x∈（0，1），f（x）＜0，求證：f（x）在（-1，1）上單調遞減；
（3）在（2）的條件下解不等式：
f
（
x
2
+
x
-
1
）
+
f
（
1
2
-
1
2
x
）
＞
0
．
組卷：309引用：3難度：0.5
解析