2023年江蘇省鎮江中學高考數學二模試卷
發布:2024/4/20 14:35:0
一、選擇題:本題共8小題,每小題5分,共40分.在每小題給出的四個選項中,只有一項是符合題目要求的.
-
1.記集合M={x||x|>2},
,則(?RM)∩N=( )N={x|y=2-x}A.{x|-2≤x≤2} B.{x|x>2} C.{x|0≤x<2} D.{x|x<-2} 組卷:57引用:3難度:0.7 -
2.設復數z滿足iz=1+i,則|z2
|=( )-zzA.0 B. 2C.2 D.2 2組卷:131引用:4難度:0.8 -
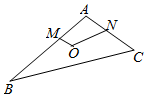 3.在如圖的平面圖形中,已知OM=1,ON=2,∠MON=120°,=2BM,MA=2CN,則NABC的值為( )?OM
3.在如圖的平面圖形中,已知OM=1,ON=2,∠MON=120°,=2BM,MA=2CN,則NABC的值為( )?OMA.-15 B.-9 C.-6 D.0 組卷:7910引用:21難度:0.5 -
4.圖1是世界上單口徑最大、靈敏度最高的射電望遠鏡“中國天眼”——500m口徑拋物面射電望遠鏡,反射面的主體是一個拋物面(拋物線繞其對稱軸旋轉所形成的曲面稱為拋物面),其邊緣距離底部的落差約為156.25米,它的一個軸截面是一個開口向上的拋物線C的一部分,放入如圖2所示的平面直角坐標系xOy內,已知該拋物線上點P到底部水平線(x軸)距離為125m,則點P到該拋物線焦點F的距離為( )
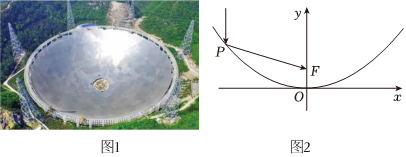
A.225m B.275m C.300m D.350m 組卷:90引用:3難度:0.7 -
5.某公園有如圖所示A至H共8個座位,現有2個男孩2個女孩要坐下休息,要求相同性別的孩子不坐在同一行也不坐在同一列,則不同的坐法總數為( )
A B C D E F G H A.168 B.336 C.338 D.84 組卷:417引用:6難度:0.7 -
6.已知函數
,記等差數列{an}的前n項和為Sn,若f(a3+2)=102,f(a2021+2)=-100,則S2023=( )f(x)=13x3+ex-e-x+1A.-4046 B.-2023 C.2023 D.4046 組卷:94引用:2難度:0.5 -
7.已知函數
在f(x)=sinωx+3cosωx(ω>0)上存在零點,且在(0,π3)上單調,則ω的取值范圍為( )(π2,3π4)A.(2,4] B. [2,72]C. [73,269]D. [73,4]組卷:432引用:5難度:0.6
四、解答題:本題共6小題,共70分.解答應寫出文字說明、證明過程或演算步驟.
-
21.已知雙曲線C:
的右頂點為A,左焦點F(-c,0)到其漸近線bx+ay=0的距離為2,斜率為x2a2-y2b2=1(0<a<10,b>0)的直線l1交雙曲線C于A,B兩點,且|AB|=13.8103
(1)求雙曲線C的方程;
(2)過點T(6,0)的直線l2與雙曲線C交于P,Q兩點,直線AP,AQ分別與直線x=6相交于M,N兩點,試問:以線段MN為直徑的圓是否過定點?若過定點,求出定點的坐標;若不過定點,請說明理由.組卷:215引用:2難度:0.4 -
22.已知函數f(x)=ex+xcosx.
(1)求函數f(x)在x=0處的切線方程;
(2)判斷函數f(x)在[0,+∞)上的單調性,并說明理由;
(3)對任意的x≥0,ex+xsinx+cosx≥ax+2,求實數a的取值范圍.組卷:162引用:2難度:0.6


