2022-2023學年重慶市永川區北山中學高三（上）期末數學試卷

一、單項選擇題（本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．）

• 1．設集合A={x∈Z|x²-2x-3≤0}，B={0，1}，則?_AB=（　　）

  A．{-3，-2，-1}

  B．{-1，2，3}

  C．{-1，0，1，2，3}

  D．{0，1}
  組卷：79引用：9難度：0.9

  解析

• 2．在復平面內，復數z=

  i

  1

  +

  2

  i

  的共軛復數對應的點位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：85引用：9難度：0.8

  解析

• 3．下列函數既是奇函數又在（-1，1）上是增函數的是（　　）

  A．y=sinx

  B． y = - 2 x

  C．y=2x+2-x

  D．y=lg（x+1）
  組卷：249引用：3難度：0.8

  解析

• 4．若（1-x）⁸=a₀+a₁（1+x）+a₂（1+x）²+…+a₈（1+x）⁸，則a₆=（　　）

  A．-448

  B．-112

  C．112

  D．448
  組卷：924引用：6難度：0.8

  解析

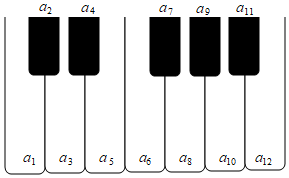• 5．如圖，將鋼琴上的12個鍵依次記為a₁，a₂，…，a₁₂．設1≤i＜j＜k≤12．若k-j=3且j-i=4，則a_i，a_j，a_k為原位大三和弦；若k-j=4且j-i=3，則稱a_i，a_j，a_k為原位小三和弦．用這12個鍵可以構成的原位大三和弦與原位小三和弦的個數之和為（　　）

  A．5

  B．8

  C．10

  D．15
  組卷：3286引用：8難度：0.8

  解析

• 6．f（x）是定義在R上的函數，

  f

  （

  x

  +

  1

  2

  ）

  +

  1

  2

  為奇函數，則f（2023）+f（-2022）=（　　）

  A．-1

  B． - 1 2

  C． 1 2

  D．1
  組卷：504引用：7難度：0.7

  解析

• 7．設F₁，F₂分別為雙曲線

  C

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的左、右焦點，A為雙曲線的左頂點，以F₁F₂為直徑的圓交雙曲線的某條漸近線于M，N兩點，且

  ∠

  MAN

  =

  3

  π

  4

  ，則該雙曲線的離心率為（　　）

  A． 2

  B． 3

  C．2

  D． 5
  組卷：364引用：6難度：0.5

  解析

四、解答題（本大題共6個大題，共70分．解答應寫出文字說明、證明過程或演算步驟．）

• 21．設橢圓

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的右焦點為F，右頂點為A，已知橢圓離心率為

  1

  2

  ，過點F且與x軸垂直的直線被橢圓截得的線段長為3．
  （Ⅰ）求橢圓C的方程
  （Ⅱ）設過點A的直線l與橢圓C交于點B（B不在x軸上），垂直于l的直線與l交于點M，與y軸交于點H，若BF⊥HF，且∠MOA≤∠MAO，求直線l斜率的取值范圍．
  組卷：89引用：2難度：0.4

  解析

• 22．已知函數f（x）=xe^x，e為自然對數的底數．
  （1）若x=-1是函數F（x）=f（x）-a（x³-3x）（a＞0）的唯一極值點，求正實數a的取值范圍；
  （2）令函數G（x）=f（x）-m（x+lnx）（m＞0），若存在實數x₁，x₂，使得G（x₁）=G（x₂），證明：x₁e

  x

  1

  +x₂e

  x

  2

  ＞2m.
  組卷：71引用：1難度：0.2

  解析