2022-2023學年江蘇省鎮江中學高三(上)月考數學試卷(10月份)
發布:2024/8/16 17:0:1
一、單項選擇題(共8小題,每小題5分.在每小題給出的四個選項中,只有一項是符合題目要求的)
-
1.
,則A∩B=( )A={x||x|≥1},B={x|x-5x-1≤0,x∈N}A.[1,5] B.(1,5] C.{0,1,2,3,4,5} D.{2,3,4,5} 組卷:226引用:3難度:0.8 -
2.已知
,a=(λ,-1),且b=(2,3),則λ=( )(a+2b)∥bA. -32B. -23C. 32D. 23組卷:2引用:2難度:0.8 -
3.平面直角坐標系中,角α的終邊經過點P(-3,4),則
=( )cos2(α2+π)A. 110B. 15C. 45D. 910組卷:168引用:5難度:0.8 -
4.已知等比數列{an}的公比q>1,前n項和為Sn,a1=1,a2+a3=6,則S5=( )
A.29 B.30 C.31 D.32 組卷:259引用:3難度:0.9 -
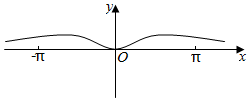 5.已知函數f(x)=x2,g(x)=ex+e-x(e為自然對數的底數),則圖像為如圖的函數可能是( )
5.已知函數f(x)=x2,g(x)=ex+e-x(e為自然對數的底數),則圖像為如圖的函數可能是( )A.y=f(x)+g(x) B.y=f(x)-g(x) C.y=f(x)g(x) D. y=f(x)g(x)組卷:72引用:4難度:0.6 -
6.若非零實數a,b滿足a<b,則下列不等式不一定成立的是( )
A. <1abB. +ba≥2abC. 1ab2<1a2bD.a2+a<b2+b 組卷:1514引用:29難度:0.7 -
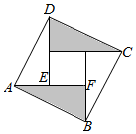 7.我國東漢數學家趙爽在《周髀算經》中利用一幅“弦圖”給出了勾股定理的證明,后人稱其為“趙爽弦圖”,它是由四個全等的直角三角形與一個小正方形拼成的一個大正方形,如圖所示,在“趙爽弦圖”中,若=AB,a=AD,b=AE34,則AF=( )EF
7.我國東漢數學家趙爽在《周髀算經》中利用一幅“弦圖”給出了勾股定理的證明,后人稱其為“趙爽弦圖”,它是由四個全等的直角三角形與一個小正方形拼成的一個大正方形,如圖所示,在“趙爽弦圖”中,若=AB,a=AD,b=AE34,則AF=( )EFA. 37+a47bB. 325+a425bC. 425+a325bD. 47+a37b組卷:185引用:5難度:0.6
三、解答題(本大題共5小題,共70分.解答應寫出文字說明、證明過程或演算步驟)
-
20.已知數列{an},{bn}的各項均為正數,前n項和分別為Sn,Tn,且對任意正整數,2an=Sn+1,2
=bn+1恒成立.Tn
(1)分別求數列{an},{bn}的通項公式;
(2)若對于任意的正整數n,Tn≤k(Sn+1)恒成立,求實數k的取值范圍.組卷:86引用:3難度:0.5 -
21.已知函數f(x)=lnx,g(x)=kx2-2x(k∈R).
(1)若y=f(x)在x=1處的切線也是y=g(x)的切線,求k的值;
(2)若x∈(0,+∞),f(x)≤g(x)恒成立,求k的最小整數值.組卷:125引用:3難度:0.3


