2022年陜西省西安市雁塔區曲江一中中考數學五模試卷

一、選擇題（本大題共7小題，每小題3分，共21分，在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．下面四個數中，最小的數是（　　）

  A．-1

  B． 5

  C．0

  D．-3
  組卷：63引用：1難度：0.7

  解析

• 2．下面的圖形是用數學家的名字命名的，其中既是軸對稱圖形，又是中心對稱圖形的是（　　）

  A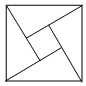． 趙爽弦圖	B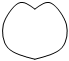． 笛卡爾心形線
  C． 科克曲線	D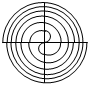． 費馬螺線
  組卷：178引用：6難度：0.9

  解析

• 3．下列各式中，計算結果是a⁸的是（　　）

  A．a9-a

  B．a16÷a2

  C．a4?a2

  D．（-a2）4
  組卷：179引用：4難度：0.7

  解析

• 4．如圖，把一個含有45°角的直角三角板放在兩條平行線m,n上，若∠α=123°，則∠β的度數是（　　）

  A．84°

  B．81°

  C．78°

  D．75°
  組卷：84引用：2難度：0.7

  解析

• 5．若一次函數y=kx+2的y隨x的增大而減少，則該函數圖象可能經過的點的坐標是（　　）

  A．（2，5）

  B．（1，1）

  C．（-1，-2）

  D．（-2，0）
  組卷：293引用：3難度：0.6

  解析

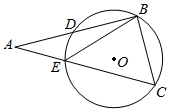• 6．如圖，在Rt△ABC中，∠ABC=90°，∠A=32°，點B、C在⊙O上，邊AB、AC分別交⊙O于D、E兩點，點B是

  ?

  CD

  的中點，則∠ABE的度數是（　　）

  A．13°

  B．16°

  C．18°

  D．21°
  組卷：1792引用：6難度：0.6

  解析

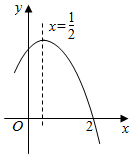• 7．二次函數y=ax²+bx+c（a≠0）的部分圖象如圖所示，對稱軸為直線x=

  1

  2

  ，且經過點（2.0）．下列說法：①abc＜0；②-2b+c=0；③4a+2b+c＜0；④若（-

  1

  2

  ，y₁），（

  5

  2

  ，y₂）是拋物線上的兩點，則y₁＜y₂；⑤

  1

  4

  b＞m（am+b）（其中m≠

  1

  2

  ）．其中正確的結論有（　　）

  A．2

  B．3

  C．4

  D．5
  組卷：1445引用：4難度：0.5

  解析

二、填空題（本大題共6小題，每小題3分，共18分）

• 8．4是

  的算術平方根．
  組卷：8581引用：332難度：0.7

  解析

• 9．用一條寬度相等的足夠長的紙條打一個結（如圖①所示），然后輕輕拉緊，壓平后可以得到如圖②的正
  五邊形ABCDE．則圖②中∠EAC的度數為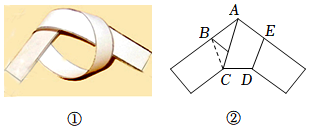

  ．
  
  組卷：263引用：4難度：0.8

  解析

三、解答題（共14小題，共81分解答應寫出過程）

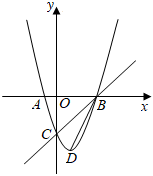• 26．如圖，在平面直角坐標系中，拋物線y=ax²+bx+c與x軸交于點A（-1，0）和點B，與y軸交于點C，頂點D的坐標為（1，-4）．
  （1）求拋物線的解析式；
  （2）若點P在拋物線上且滿足∠PCB=∠CBD，求點P的坐標．
  組卷：586引用：1難度：0.2

  解析

• 27．問題提出
  （1）如圖1，在四邊形ABCD中，已知∠A=60°，∠B=150°，AB=3，AD=4，BC=2

  3

  ，求四邊形ABCD的面積．（結果保留根號）
  問題探究
  （2）某地有兩條平行的道路m、n,以及與其相交的另一條道路l,交點分別為A、B兩點（如圖2所示），在道路m、n上分別有一點P、Q，且AP=60m,BQ=180m,AB=240m,∠ABQ=60°，現計劃在道路m、n之間，道路1右側選取兩點M、N，修建四邊形花園PMQN，且滿足PM=PN，∠MPN=120°，∠MQN=30°，想使得這個花園（四邊形PMQN）的面積最小，試問：是否存在符合要求的四邊形PMQN？若存在，請求出其面積的最小值；若不存在，請說明理由．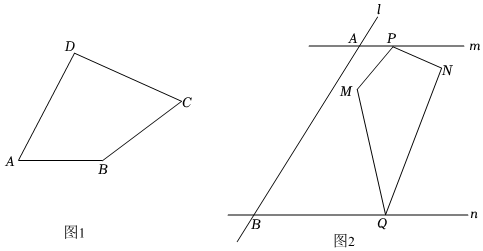
  
  組卷：337引用：1難度：0.2

  解析