2020-2021學年黑龍江省哈爾濱122中學高一（上）期中數(shù)學試卷

一、單項選擇題

• 1．若不等式

  （

  1

  2

  ）

  a

  +

  1

  ＜

  （

  1

  2

  ）

  3

  -

  3

  a

  成立，則a的取值范圍（　　）

  A．（1，+∞）

  B． （ 1 2 ， + ∞ ）

  C．（-∞，1）

  D． （ - ∞ ， 1 2 ）
  組卷：24引用：1難度：0.8

  解析

• 2．若a＞b＞0，c＞d＞0，則下列不等式一定成立的是（　　）

  A．a(chǎn)c＞bd

  B．a(chǎn)c＜bd

  C．a(chǎn)d＜bd

  D．a(chǎn)d＞bc
  組卷：7引用：1難度：0.8

  解析

• 3．已知函數(shù)f（x）=（m²-m-5）x^m-1是冪函數(shù)，且f（x）在（0，+∞）單調(diào)遞增，則m的值為（　　）

  A．-2

  B．3

  C．-2或3

  D．2或3
  組卷：26引用：2難度：0.8

  解析

• 4．若函數(shù)y=

  2 - x - 1 ， x ≤ 0

  x 1 2 ， x ＞ 0

  ，當x=x₀時函數(shù)值y＞1，則x₀的取值范圍是（　　）

  A．（-1，1）	B．（-1，+∞）
  C．（-∞，-2）∪（0，+∞）	D．（-∞，-1）∪（1，+∞）
  組卷：4引用：1難度：0.7

  解析

• 5．已知f（x），g（x）分別是定義在R上的偶函數(shù)和奇函數(shù)，且f（x）-g（x）=x³+x²+1，則f（1）+g（1）=（　　）

  A．-3

  B．-1

  C．1

  D．3
  組卷：7258引用：103難度：0.9

  解析

• 6．已知函數(shù)f（x）=

  a

  x

  2

  +

  4

  ax

  +

  4

  的定義域為R，則實數(shù)a的取值范圍為（　　）

  A．（0，1]	B．（-∞，0]∪[1，+∞）
  C．（-∞，0）∪（1，+∞）	D．[0，1]
  組卷：226引用：7難度：0.9

  解析

• 7．若函數(shù)

  f

  （

  x

  ）

  =

  （

  1

  5

  ）

  x

  2

  +

  ax

  在[1，2]單調(diào)遞減，則a的取值范圍（　　）

  A．a(chǎn)≤-4

  B．a(chǎn)≤-2

  C．a(chǎn)≥-2

  D．a(chǎn)≥-4
  組卷：16引用：2難度：0.7

  解析

四、解答題

• 21．（1）已知x＞1，求

  f

  （

  x

  ）

  =

  x

  2

  +

  3

  x

  x

  -

  1

  最小值；
  （2）已知a＞0，b＞0，a+b=4，求

  9

  a

  +

  1

  +

  1

  b

  +

  1

  的最小值并求出此時a,b的值．
  組卷：121引用：1難度：0.6

  解析

• 22．某蔬菜基地種植西紅柿，由歷年市場行情得知，從二月一日起的300天內(nèi)，西紅柿市場售價與上市時間的關系用圖1所示的一條折線表示，西紅柿的種植成本與上市時間的關系用圖2所示的拋物線表示．（注：市場售價和種植成本的單位：元/kg,時間單位：天）
  
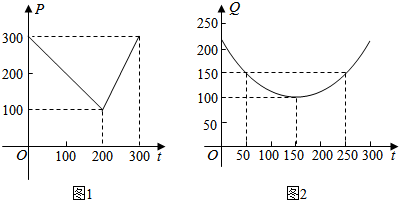
  （1）寫出圖1表示的市場售價與時間的函數(shù)關系式P=f（t）；寫出圖2表示的種植成本與時間的函數(shù)關系式Q=g（t）；
  （2）認定市場售價減去種植成本為純收益，問何時上市的西紅柿純收益最大？為多少？
  組卷：195引用：8難度：0.5

  解析