當前位置：試卷中心 > 試卷詳情

2023-2024學年江蘇省無錫一中高二（上）質檢數學試卷

發布：2024/9/11 5:0:9

一．單選題（每題5分，共40分）

1．直線
y
=
π
2
的傾斜角為（　　）
A．180° B．0° C．90° D．不存在
組卷：58引用：3難度：0.8
解析
2．已知直線l₁：ax+y+a=0與l₂：（a-6）x+（a-4）y-4=0，則“a=2”是“l₁∥l₂”的（　　）
A．充分不必要條件 B．必要不充分條件
C．充要條件 D．既不充分也不必要條件
組卷：185引用：7難度：0.8
解析
3．已知x+y=0，則
x
2
+
y
2
-
2
x
-
2
y
+
2
+
（
x
-
2
）
2
+
y
2
的最小值為（　　）
A．
5
B．2
2
C．
10
D．2
5
組卷：225引用：18難度：0.6
解析
4．已知點M（x₀，y₀）在圓x²+y²=2外，則直線x₀x+y₀y=2與圓的位置關系是（　　）
A．相切 B．相交 C．相離 D．不確定
組卷：169引用：5難度：0.5
解析
5．已知F₁，F₂是橢圓
x
2
25
+
y
2
16
=
1
的兩個焦點，P是橢圓上一點，則|PF₁|?|PF₂|的最大值是（　　）
A．
25
4
B．9 C．16 D．25
組卷：1218引用：9難度：0.7
解析
6．瑞士數學家歐拉（Leonhard Euler）1765年在其所著的《三角形的幾何學》一書中提出：任意三角形的外心、重心、垂心在同一條直線上．后人稱這條直線為歐拉線．已知△ABC的頂點A（2，0），B（0，2），其歐拉線方程為2x-y-2=0，則頂點C的坐標是（　　）
A．（
18
5
，
16
5
） B．（
16
5
，
18
5
）
C．（
36
13
，
50
13
） D．（
50
13
，
36
13
）
組卷：91引用：7難度：0.7
解析
7．如圖①，用一個平面去截圓錐得到的截口曲線是橢圓．許多人從純幾何的角度出發對這個問題進行過研究，其中比利時數學家Germinaldandelin（1794-1847）的方法非常巧妙，極具創造性．在圓錐內放兩個大小不同的球，使得它們分別與圓錐的側面、截面相切，兩個球分別與截面相切于E、F，在截口曲線上任取一點A，過A作圓錐的母線，分別與兩個球相切于C、B，由球和圓的幾何性質，可以知道，AE=AC，AF=AB，于是AE+AF=AB+AC=BC．由B、C的產生方法可知，它們之間的距離BC是定值，由橢圓定義可知，截口曲線是以E、F為焦點的橢圓．

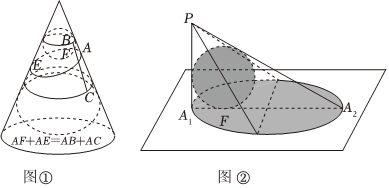
如圖②，一個半徑為2的球放在桌面上，桌面上方有一個點光源P，則球在桌面上的投影是橢圓，已知A₁A₂是橢圓的長軸，PA₁垂直于桌面且與球相切，PA₁=5，則橢圓的焦距為（　　）
A．4 B．6 C．8 D．12
組卷：167引用：2難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四．解答題（共70分）

21．在平面直角坐標系中，曲線E的軌跡方程為x²+y²=4．
（1）若直線l：y=kx-4與曲線E交于不同的兩點C，D，且∠OCD=30°（O為坐標原點），求直線l的斜率；
（2）若點Q是直線l：x-y-4=0上的動點，過Q作曲線E的兩條切線QM，QN，切點為M，N，探究：直線MN是否過定點．
組卷：47引用：3難度：0.5
解析
22．規定：在桌面上，用母球擊打目標球，使目標球運動，球的位置是指球心的位置我們說球A是指該球的球心點A．兩球碰撞后，目標球在兩球的球心所確定的直線上運動，目標球的運動方向是指目標球被母球擊打時，母球球心所指向目標球球心的方向．所有的球都簡化為平面上半徑為1的圓，且母球與目標球有公共點時，目標球就開始運動，在桌面上建立平面直角坐標系，解決下列問題：
（1）如圖1，設母球A的位置為（0，0），目標球B的位置為（4，0），要使目標球B向C（8，-4）處運動，求母球A球心運動的直線方程；
（2）如圖2，若母球A的位置為（0，-2），目標球B的位置為（4，0），能否讓母球A擊打目標B球后，使目標B球向（8，-4）處運動？
（3）若A的位置為（0，a）時，使得母球A擊打目標球B時，目標球B（
4
2
，0）運動方向可以碰到目標球C（
7
2
，
-
5
2
），求a的最小值（只需要寫出結果即可）．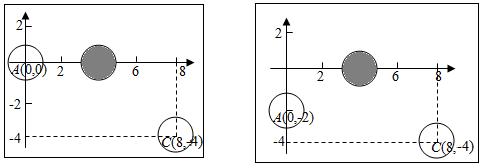
組卷：56引用：7難度：0.6
解析