2021-2022學年北京人大附中九年級（上）開學調研數學試卷

一、選擇題（3×10=30分）

• 1．剪紙是我國最古老的民間藝術之一，有著悠久的歷史，已經在某種意義上成為了中國文化的一種象征．剪紙是一種鏤空藝術，在視覺上給人以透空的感覺和藝術享受．下列剪紙作品中，是中心對稱圖形的為（　　）

  A．	B．
  C．	D．
  組卷：84引用：4難度：0.8

  解析

• 2．用配方法解一元二次方程x²-4x-5=0的過程中，配方正確的是（　　）

  A．（x+2）2=1

  B．（x-2）2=1

  C．（x+2）2=9

  D．（x-2）2=9
  組卷：1317引用：69難度：0.9

  解析

• 3．若點（-1，y₁），（2，y₂），（3，y₃）都在反比例函數y=

  6

  x

  的圖象上，則（　　）

  A．y1＜y2＜y3

  B．y2＜y1＜y3

  C．y3＜y2＜y1

  D．y1＜y3＜y2
  組卷：511引用：4難度：0.5

  解析

• 4．已知函數

  y

  =

  1

  2

  x

  2

  -

  x

  -

  4

  ，當函數值y隨x的增大而減小時，x的取值范圍是（　　）

  A．x＜1

  B．x＞1

  C．x＞-2

  D．-2＜x＜4
  組卷：416引用：17難度：0.9

  解析

• 5．如圖，在Rt△ACB中，∠ACB=90°，∠A=35°，將△ABC繞點C逆時針旋轉α角到△A₁B₁C的位置，A₁B₁恰好經過點B，則旋轉角α的度數等（　　）

  A．70°

  B．65°

  C．55°

  D．35°
  組卷：824引用：9難度：0.5

  解析

• 6．若二次函數y=kx²-4x-2與x軸有兩個交點，則k的取值范圍是（　　）

  A．k＞-2

  B．k＞-2且k≠0

  C．k＜2

  D．k≥-2且k≠0
  組卷：720引用：5難度：0.6

  解析

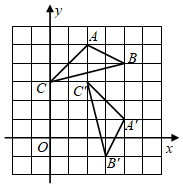• 7．如圖，將△ABC繞點P順時針旋轉得到△A'B'C'，則點P的坐標為（　　）

  A．（1，1）

  B．（1，2）

  C．（1，3）

  D．（1，4）
  組卷：966引用：12難度：0.6

  解析

• 8．將拋物線y=2x²+1繞原點O旋轉180°，則旋轉后的拋物線的解析式為（　　）

  A．y=-2x2

  B．y=-2x2+1

  C．y=2x2-1

  D．y=-2x2-1
  組卷：152引用：2難度：0.7

  解析

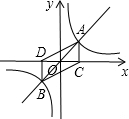• 9．如圖，點A、B是函數y=x與y=

  1

  x

  的圖象的兩個交點，作AC⊥x軸于C，作BD⊥x軸于D，則四邊形ACBD的面積為（　　）

  A．S＞2

  B．S＞1

  C．S＜1

  D．S=2
  組卷：247引用：4難度：0.9

  解析

三、解答題

• 27．在正方形ABCD中，E是CD邊上一點．
  
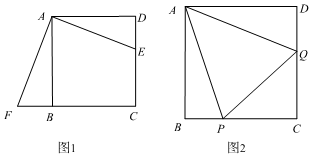
  （1）將△ADE繞點A順時針旋轉90°得到△ABF，如圖1所示，觀察可知，與DE相等的線段是

  ，∠AFB=

  ．
  （2）如圖2，在正方形ABCD中，P、Q分別是BC、CD邊上的點，且∠PAQ=45°，猜想線段DQ、BP、PQ的數量關系，并證明；
  （3）在圖2中，連接BD分別交AP、AQ于點M，N，直接寫出BM、DN、MN的數量關系．
  組卷：172引用：4難度：0.1

  解析

• 28．在平面直角坐標系xOy中，對于與坐標軸不平行的直線l和點P，給出如下定義：過點P作x軸，y軸的垂線，分別交直線l于點M，N，若PM+PN＞2，則稱P為直線的平安點．已知點A（-

  2

  ，0），B（0，1），C（-1，1）．
  （1）當直線l的表達式為y=x時，
  ①在點A，B，C中，直線的平安點是

  ；
  ②若以OB為邊的矩形OBEF上存在直線l的平安點，求點E的橫坐標n的取值范圍；
  （2）當直線的表達式為y=kx時，若點C是直線l的平安點，求k的取值范圍．
  組卷：375引用：4難度：0.5

  解析