2023-2024學年江蘇省南京師大附中江寧分校八年級（上）月考數學試卷（10月份）

一、選擇題（共10小題，每小題2分，共20分）

• 1．以下四家銀行的行標圖中，是軸對稱圖形的有（　　）
  

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：626引用：36難度：0.9

  解析

• 2．下列說法正確的是（　　）

  A．形狀相同的兩個三角形全等

  B．面積相等的兩個三角形全等

  C．完全重合的兩個三角形全等

  D．所有的等邊三角形全等
  組卷：229引用：12難度：0.6

  解析

• 3．如圖，已知AB⊥BC，BC⊥CD，AB=DC，則可以判定△ABC≌△DCB的根據是（　　）

  A．HL

  B．ASA

  C．SAS

  D．AAS
  組卷：189引用：2難度：0.8

  解析

• 4．在聯歡會上，有A、B、C三名選手站在一個三角形的三個頂點位置上，他們在玩“搶凳子”游戲，要求在他們中間放一個木凳，誰先搶到凳子誰獲勝，為使游戲公平，則凳子應放的最適當的位置是在△ABC的（　　）

  A．三邊垂直平分線的交點	B．三條中線的交點
  C．三條角平分線的交點	D．三條高所在直線的交點
  組卷：1292引用：47難度：0.6

  解析

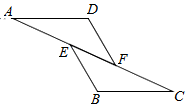• 5．如圖，已知AE=CF，∠AFD=∠CEB，那么添加下列一個條件后，仍無法判定△ADF≌△CBE的是（　　）

  A．∠B=∠D

  B．BE=DF

  C．AD=CB

  D．AD∥BC
  組卷：138引用：5難度：0.7

  解析

• 6．如圖，DE是△ABC的邊BC的垂直平分線，分別交邊AB，BC于點D，E，且AB=9，AC=6，則△ACD的周長是（　　）

  A．10.5

  B．12

  C．15

  D．18
  組卷：2086引用：22難度：0.7

  解析

• 7．如圖所示，已知AB=CD，AD=CB，AC、BD相交于O，則圖中全等三角形有（　　）

  A．2對

  B．3對

  C．4對

  D．5對
  組卷：672引用：29難度：0.9

  解析

• 8．平面上有△ACD與△BCE，其中AD與BE相交于P點，如圖．若AC=BC，AD=BE，CD=CE，∠ACE=55°，∠BCD=155°，則∠BPD的度數為（　　）

  A．110°

  B．125°

  C．130°

  D．155°
  組卷：5451引用：86難度：0.5

  解析

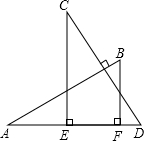• 9．如圖，AB⊥CD，且AB=CD；E、F是AD上的兩點，連接CE，BF，CE⊥AD，BF⊥AD，若CE=a,BF=b,EF=c,則AD的長為（　　）

  A．a-b+c

  B．a+b-c

  C．a+c

  D．b+c
  組卷：441引用：3難度：0.7

  解析

三、解答題（共7小題）

• 26．在△ABC中，∠ACB=90°，AC=BC，直線MN經過點C，且AD⊥MN于D，BE⊥MN于E．
  （1）當直線MN繞點C旋轉到圖1的位置時，
  求證：①△ADC≌△CEB；
  ②DE=AD+BE；
  （2）當直線MN繞點C旋轉到圖2的位置時，（1）中的結論還成立嗎？若成立，請給出證明；若不成立，說明理由．
  
  組卷：11586引用：37難度：0.3

  解析

• 27．【問題引領】
  
  問題1：如圖1，在四邊形ABCD中，CB=CD，∠B=∠ADC=90°，∠BCD=120°，E，F分別是AB，AD上的點，且∠ECF=60°．探究圖中線段BE，EF，FD之間的數量關系．
  小王同學探究此問題的方法是，延長FD到點G．使DG=BE．連結CG，先證明△CBE≌△CDG，再證明△CEF≌△CGF．他得出的正確結論是

  ．
  【探究思考】
  問題2：如圖2，若將問題1的條件改為：四邊形ABCD中，CB=CD，∠ABC+∠ADC=180°，∠ECF=

  1

  2

  ∠BCD，問題1的結論是否仍然成立？請說明理由．
  【拓展延伸】
  問題3：如圖3，在問題2的條件下，若點E在AB的延長線上，點F在DA的延長線上，若BE=2，DF=8，求EF的長．（請直接寫出答案）
  組卷：346引用：4難度：0.1

  解析