人教A版（2019）選擇性必修第一冊《1.2 空間向量基本定理》2020年同步練習(xí)卷（5）

一、選擇題

• 1．若向量

  {

  a

  ，

  b

  ，

  c

  }

  是空間的一個基底，則一定可以與向量

  p

  =

  2

  a

  +

  b

  ，

  q

  =

  2

  a

  -

  b

  構(gòu)成空間的另一個基底的向量是（　　）

  A． a

  B． b

  C． c

  D． a + b
  組卷：106引用：3難度：0.9

  解析

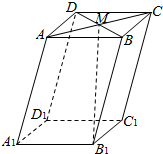• 2．如圖，在平行六面體ABCD-A₁B₁C₁D₁中，M為AC與BD的交點，若

  A

  1

  B

  1

  =

  a

  ，

  A

  1

  D

  1

  =

  b

  ，

  A

  1

  A

  =

  c

  ．則下列向量中與

  B

  1

  M

  相等的向量是（　　）

  A．- 1 2 a + 1 2 b + c

  B． 1 2 a + 1 2 b + c

  C． 1 2 a - 1 2 b + c

  D．- 1 2 a - 1 2 b + c
  組卷：1939引用：110難度：0.9

  解析

• 3．若向量

  MA

  ，

  MB

  ，

  MC

  的起點M和終點A，B，C互不重合，且無三點共線，O為空間任意一點，則能使向量

  MA

  ，

  MB

  ，

  MC

  成為空間一個基底的關(guān)系式是（　　）

  A． OM = 1 3 OA + 1 3 OB + 1 3 OC	B． MA = MB + MC
  C． OM = OA + OB + OC	D． MA = 2 MB - MC
  組卷：136引用：9難度：0.7

  解析

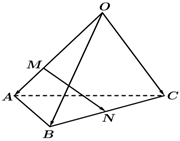• 4．如圖所示，在四面體O-ABC中，

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，點M在OA上，且

  OM

  =2

  MA

  ，N為BC的中點，則

  MN

  =（　　）

  A． 1 2 a - 2 3 b + 1 2 c	B．- 2 3 a + 1 2 b + 1 2 c
  C． 1 2 a + 1 2 b - 2 3 c	D． 2 3 a + 2 3 b - 1 2 c
  組卷：1254引用：41難度：0.9

  解析

• 5．平行六面體ABCD-A₁B₁C₁D₁中，向量

  AB

  、

  AD

  、

  A

  A

  1

  兩兩的夾角均為60°，且|

  AB

  |=1，|

  AD

  |=2，|

  A

  A

  1

  |=3，則|

  A

  C

  1

  |等于（　　）

  A．5

  B．6

  C．4

  D．8
  組卷：478引用：15難度：0.7

  解析

五、填空題

• 14．已知

  e

  1

  ，

  e

  2

  是空間單位向量，

  e

  1

  ?

  e

  2

  =

  1

  2

  ，若空間向量

  b

  滿足

  b

  ?

  e

  1

  =

  2

  ，

  b

  ?

  e

  2

  =

  5

  2

  ，且對于任意x,y∈R，

  |

  b

  -

  （

  x

  e

  1

  +

  y

  e

  2

  ）

  |

  ≥

  |

  b

  -

  （

  x

  0

  e

  1

  +

  y

  0

  e

  2

  ）

  |

  =1（x₀，y₀∈R），則x₀=

  ，y₀=

  ，

  |

  b

  |=

  ．
  組卷：2288引用：2難度：0.5

  解析

• 15．在平行六面體ABCDA₁B₁C₁D₁中，設(shè)

  AB

  =

  a

  ，

  AD

  =

  b

  ，

  A

  A

  1

  =

  c

  ，E，F(xiàn)分別是AD₁，BD的中點．
  （1）用向量

  a

  ，

  b

  ，

  c

  表示

  D

  1

  B

  ，

  EF

  ；
  （2）若

  D

  1

  F

  =x

  a

  +y

  b

  +z

  c

  ，求實數(shù)x,y,z的值．
  組卷：211引用：24難度：0.5

  解析