2022年安徽省合肥市高考數(shù)學(xué)一模試卷

一、選擇題：本大題共12小題，每小題5分，滿分60分，在每小題給出的四個選項(xiàng)中，只有

• 1．集合M={x|1＜x＜4}，N={x|2≤x≤3}，則M∩N=（　　）

  A．{x|2≤x＜4}

  B．{x|2≤x≤3}

  C．{x|1＜x≤3}

  D．{x|1＜x＜4}
  組卷：43引用：3難度：0.7

  解析

• 2．復(fù)數(shù)

  i

  1

  +

  i

  （i為虛數(shù)單位）在復(fù)平面上對應(yīng)的點(diǎn)位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：33引用：5難度：0.9

  解析

• 3．若向量

  a

  ，

  b

  為單位向量，|

  a

  -2

  b

  |=

  7

  ，則向量

  a

  與向量

  b

  的夾角為（　　）

  A．30°

  B．60°

  C．120°

  D．150°
  組卷：720引用：5難度：0.7

  解析

• 4．函數(shù)y=

  sin

  |

  2

  x

  |

  x

  2

  +

  1

  在[-π，π]的圖象大致為（　　）

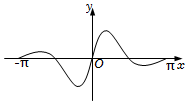
  A．	B．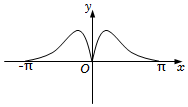
  C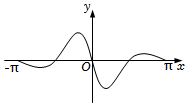．	D．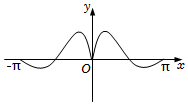
  組卷：301引用：8難度：0.7

  解析

• 5．在高一入學(xué)時，某班班委統(tǒng)計(jì)了本班所有同學(xué)中考體育成績的平均分和方差．后來又轉(zhuǎn)學(xué)來一位同學(xué)．若該同學(xué)中考體育的成績恰好等于這個班級原來的平均分，則下列說法正確的是（　　）

  A．班級平均分不變，方差變小

  B．班級平均分不變，方差變大

  C．班級平均分改變，方差變小

  D．班級平均分改變，方差變大
  組卷：232引用：5難度：0.8

  解析

• 6．若sinα=

  1

  3

  ，α∈

  （

  π

  2

  ，

  π

  ）

  ，則sin（α-

  3

  π

  2

  ）的值為（　　）

  A．- 1 3

  B．- 2 2 3

  C． 1 3

  D． 2 2 3
  組卷：320引用：3難度：0.7

  解析

• 7．若直線l：x-2y-

  15

  =0經(jīng)過雙曲線M：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1的一個焦點(diǎn)，且與雙曲線M有且僅有一個公共點(diǎn)，則雙曲線M的方程為（　　）

  A． x 2 5 - y 2 20 =1

  B． x 2 20 - y 2 5 =1

  C． x 2 3 - y 2 12 =1

  D． x 2 12 - y 2 3 =1
  組卷：96引用：3難度：0.5

  解析

選修4-4：坐標(biāo)系與參數(shù)方程

• 22．在平面直角坐標(biāo)系xOy中，曲線C₁的參數(shù)方程為

  x = 3 cost

  y = sint

  （t為參數(shù)）．以坐標(biāo)原點(diǎn)為極點(diǎn)，x軸的非負(fù)半軸為極軸建立極坐標(biāo)系，曲線C₂的極坐標(biāo)方程為ρ²-8ρsinθ+12=0．
  （1）求C₁的普通方程和C₂的直角坐標(biāo)方程；
  （2）點(diǎn)P是曲線C₁上的動點(diǎn)，過點(diǎn)P作直線l與曲線C₂有唯一公共點(diǎn)Q，求|PQ|的最大值．
  組卷：172引用：5難度：0.5

  解析

選修4-5：不等式選講

• 23．已知f（x）=|x-1|+|x+a|．
  （1）當(dāng)a=2時，求y=f（x）與y=6所圍成封閉圖形的面積；
  （2）若對于任意的x∈R，都存在y∈（1，+∞），使（y-1）f（x）≥y²+3成立，求a的取值范圍．
  組卷：34引用：3難度：0.6

  解析