2023年四川省內江市隆昌七中中考數學三模試卷
發布:2024/5/20 8:0:9
一、選擇題(本大題共12小題,每小題3分,共36分.在每小題給出的九個選項中,只有一項是符合題目要求的.)
-
1.如果數a與2互為相反數,那么a是( )
A.2 B.0 C.-2 D.- 23組卷:1047引用:6難度:0.7 -
2.2020年是不尋常的一年,據世衛組織統計,截止2020年6月28日全球累計已超過1040萬人確診感染了“新冠”病毒,將數據1040萬用科學記數法表示為( )
A.1040×104 B.104×105 C.1.04×107 D.1.04×108 組卷:97引用:4難度:0.9 -
3.如圖,一個正方塊的六個面分別標有A、B、C、D、E、F,從三個不同方向看到的情況如圖所示,則A的對面應該是字母( )
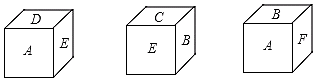
A.B B.C C.E D.F 組卷:1274引用:8難度:0.8 -
4.若單項式-amb3與2a2bn的和是單項式,則n的值是( )
A.3 B.6 C.8 D.9 組卷:319引用:2難度:0.8 -
5.函數y=
中,自變量x的取值范圍是( )x-2xA.x≠0 B.x≥2 C.x>2且x≠0 D.x≥2且x≠0 組卷:4404引用:79難度:0.5 -
6.已知非零實數x滿足x2-3x-1=0,則x2+
的值為( )1x2A.11 B.9 C.7 D.5 組卷:2193引用:12難度:0.8 -
7.按如圖所示的程序計算,若開始輸入的x值為-2,則最后輸出的結果是( )
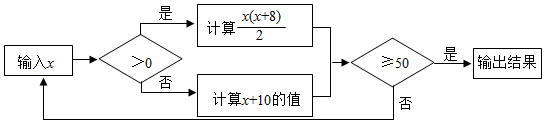
A.8 B.64 C.120 D.128 組卷:522引用:7難度:0.7 -
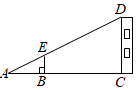 8.如圖所示,某校數學興趣小組利用標桿BE測量建筑物的高度,已知標桿BE高為1.5m,測得AB=3m,BC=7m,則建筑物CD的高是( )
8.如圖所示,某校數學興趣小組利用標桿BE測量建筑物的高度,已知標桿BE高為1.5m,測得AB=3m,BC=7m,則建筑物CD的高是( )A.3.5m B.4m C.4.5m D.5m 組卷:2010引用:17難度:0.7 -
9.設a、b、c是△ABC三邊,并且關于x的方程
x2-(a+b)x+2ab+c2=0有兩個相等的實數根,判斷△ABC的形狀,正確的結論是( )14A.等腰三角形 B.直角三角形 C.等腰直角三角形 D.正三角形 組卷:498引用:8難度:0.5
五、解答題(本大題共3個小題,每小題12分,共36分、解答題必須寫出必要的文字說明、證明過程或推演步驟)
-
27.閱讀下列材料:
我們知道|x|的幾何意義是在數軸上數x對應的點與原點的距離;即|x|=|x-0|;這個結論可以推廣為|x1-x2|表示在數軸上數x1,x2對應點之間的距離.絕對值的幾何意義在解題中有著廣泛的應用:
例1:解方程|x|=4.
容易得出,在數軸上與原點距離為4的點對應的數為±4,即該方程的解x=±4;
例2:解方程|x+1|+|x-2|=5.
由絕對值的幾何意義可知,該方程表示求在數軸上與-1和2的距離之和為5的點對應的x的值.在數軸上,-1和2的距離為3,滿足方程的x對應的點在2的右邊或在-1的左邊.若x對應的點在2的右邊,如圖1可以看出x=3;同理,若x對應點在-1的左邊,可得x=-2.所以原方程的解是x=3或x=-2.
例3:解不等式|x-1|>3.
在數軸上找出|x-1|=3的解,即到1的距離為3的點對應的數為-2,4,如圖2,在-2的左邊或在4的右邊的x值就滿足|x-1|>3,所以|x-1|>3的解為x<-2或x>4.
參考閱讀材料,解答下列問題:
(1)方程|x+3|=5的解為;
(2)方程|x-2017|+|x+1|=2020的解為;
(3)若|x+4|+|x-3|≥11,求x的取值范圍. 組卷:2892引用:3難度:0.1
組卷:2892引用:3難度:0.1 -
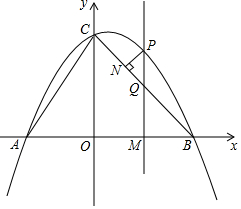 28.如圖,拋物線y=ax2+bx+4交x軸于A(-3,0),B(4,0)兩點,與y軸交于點C,連接AC,BC.點P是第一象限內拋物線上的一個動點,點P的橫坐標為m,過點P作PM⊥x軸,垂足為點M,PM交BC于點Q.
28.如圖,拋物線y=ax2+bx+4交x軸于A(-3,0),B(4,0)兩點,與y軸交于點C,連接AC,BC.點P是第一象限內拋物線上的一個動點,點P的橫坐標為m,過點P作PM⊥x軸,垂足為點M,PM交BC于點Q.
(1)求此拋物線的表達式:
(2)過點P作PN⊥BC,垂足為點N,請用含m的代數式表示線段PN的長,并求出當m為何值時PN有最大值,最大值是多少?
(3)試探究點P在運動過程中,是否存在這樣的點Q,使得以A,C,Q為頂點的三角形是等腰三角形.若存在,請求出此時點Q的坐標,若不存在,請說明理由.組卷:1508引用:4難度:0.2


