北師大新版八年級下冊《第1章 三角形的證明》2021年單元測試卷（1）
發布：2024/11/2 11:0:2
一、選擇題（本題共計7小題，每題3分，共計21分，）
-
1．等邊三角形的一個角是（ ）
組卷：77引用：1難度：0.7 -
2．如圖，矩形ABCD中，對角線AC=4，△AOB是等邊三角形，則AD的長為（ ）組卷：549引用：5難度：0.5 -
3．若直角三角形中的兩個銳角之差為22°，則較小的一個銳角的度數是（ ）
組卷：279引用：6難度：0.9 -
4．如圖所示，BE，CD是△ABC的兩條高，F為BC的中點．那△DEF是（ ）組卷：87引用：2難度：0.9 -
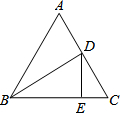5．如圖，在等邊△ABC中，BD平分∠ABC交AC于點D，過點D作DE⊥BC于點E，且CE=2，則AB的長為（ ）組卷：212引用：4難度：0.9 -
6．如圖，在△ABC中，AB=20cm,AC=12cm,點P從點B出發以每秒3cm的速度向點A運動，點Q從點A同時出發以每秒2cm的速度向點C運動，其中一個動點到達端點時，另一個動點也隨之停止運動，當∠APQ=∠AQP時，P，Q運動的時間為（ ）組卷：341引用：2難度：0.7
二、填空題（本題共計8小題，每題3分，共計24分，）
-
7．三個角都相等的三角形是
三角形．組卷：165引用：4難度：0.7
三、解答題（本題共計7小題，共計58分，）
-
20．如圖，在Rt△ABC中，CD是斜邊AB的高，求證：∠BCD=∠A．組卷：173引用：2難度：0.5 -
21．李老師給愛好學習的小兵和小鵬提出這樣一個問題：如圖1，在△ABC中，AB=AC，點P為邊BC上的任一點，過點P作PD⊥AB，PE⊥AC，垂足分別為D、E，過點C作CF⊥AB，垂足為F．求證：PD+PE=CF．
小兵的證明思路是：如圖2，連接AP，由△ABP與△ACP面積之和等于△ABC的面積可以證得：PD+PE=CF．
小鵬的證明思路是：如圖2，過點P作PG⊥CF，垂足為G，先證△GPC≌△ECP，可得：PE=CG，而PD=GF，則PD+PE=CF．
請運用上述中所證明的結論和證明思路完成下列兩題：
（1）如圖3，將長方形ABCD沿EF折疊，使點D落在點B上，點C落在點C′處，點P為折痕EF上的任一點，過點P作PG⊥BE、PH⊥BC，垂足分別為G、H，若AD=16，CF=6，求PG+PH的值；
（2）如圖4，P是邊長為6的等邊三角形ABC內任一點，且PD⊥AB，PF⊥AC，PE⊥BC，求PD+PE+PF的值．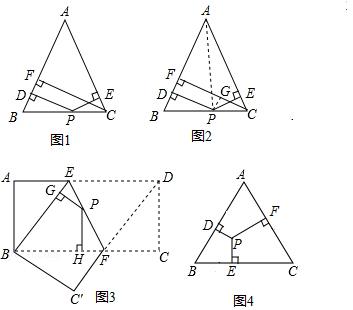
組卷：1028引用：3難度：0.1