當前位置：試卷中心 > 試卷詳情

2023-2024學年河北省保定市高三（上）摸底數學試卷（10月份）

發布：2024/9/28 11:0:2

一、選擇題。本大題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

1．已知集合A={x|x=3n-1，n∈Z}，B={x|0＜x＜6}，則A∩B=（　　）
A．（1，4） B．{1，5} C．{2，4} D．{2，5}
組卷：164引用：5難度：0.8
解析
2．若復數z滿足
2
+
z
2
-
z
=
i
，則z=（　　）
A．i B．-i C．2i D．-2i
組卷：83引用：7難度：0.8
解析
3．若角α的終邊經過點P（1，-2），則tan2α的值為（　　）
A．
4
3
B．
2
3
C．
1
2
D．-
4
3
組卷：143引用：8難度：0.9
解析
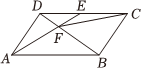4．如圖，在平行四邊形ABCD中，E是CD的中點，AE和BD相交于點F．記
AB

=
a
，
AD
=
b
，則（　　）
A．
CF
=-
2
3
a
-
1
3
b
B．
CF
=
2
3
a
+
1
3
b
C．
CF
=-
1
3
a
-
2
3
b
D．
CF
=
1
3
a
+
2
3
b
組卷：155引用：1難度：0.7
解析
5．已知a,b是異面直線，α，β是兩個平面，a?α，b?β，設p：a∥β且b∥α；q：α∥β，則（　　）
A．p是q的充分條件但不是必要條件
B．p是q的必要條件但不是充分條件
C．p是q的充要條件
D．p既不是q的充分條件也不是q的必要條件
組卷：104引用：2難度：0.5
解析
6．現有一張正方形剪紙，沿只過其一個頂點的一條直線將其剪開，得到2張紙片，再從中任選一張，沿只過其一個頂點的一條直線剪開，得到3張紙片，…，以此類推，每次從紙片中任選一張，沿只過其一個頂點的一條直線剪開，若經過10次剪紙后，得到的所有多邊形紙片的邊數總和為（　　）
A．33 B．34 C．36 D．37
組卷：30引用：5難度：0.5
解析
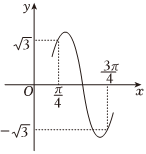7．已知函數f（x）=2cos（ωx-φ）（ω＞0，
π
2
＜φ＜
3
π
2
）的部分圖象如圖所示，則（　　）
A．f（0）=-
3
B．f（x+
π
6
）是奇函數
C．f（x）的圖象關于直線x=
π
3
對稱
D．f（x）在區間（0，
π
2
）上單調遞增
組卷：93引用：1難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題。本題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

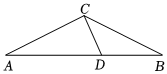21．2023年3月，保定市在城市建設管理中突出城市品質，謀劃推進“公園+”“道路+”“+生態”“+文化”工程，讓居民處處感受到精致的生活體驗，讓城市增添更多暖意、愜意、詩意．某兩個小區之間有一塊三角形空地，市政府計劃在這塊三角形空地上修建一個微型公園．如圖所示，經測量
∠
A
=∠
B
=
π
6
，
AB
=
200
3
米，修建一條景觀水渠（水渠寬度忽略不計）CD把三角形空地分成兩個區域：三角形ACD為游樂擴展區，三角形BCD為健身休閑區．已知游樂拓展區每平米造價200元，健身休閑區每平米造價100元，景觀水渠每米造價10000元．
（1）若
∠
CDA
=
π
4
，求景觀水渠CD的長度；
（2）求當∠CDA取何值時政府的總投資最少，并求出總投資最小值．
組卷：15引用：1難度：0.5
解析
22．設數列{a_n}、{b_n}的前n項和分別為A_n，B_n，且a₁=2，
A
n
=
n
+
2
3
a
n
，B_n=2-b_n．
（1）求{a_n}和{b_n}的通項公式；
（2）設
c
1
=
2
，c_n=
a
n
（b₁+b₂+…+b_n-1）+（
a
1
+
a
2
+…+
a
n
）b_n（n≥2），數列{c_n}的前n項和為S_n，證明：①S_n=（
a
1
+
a
2
+…+
a
n
）?（b₁+b₂+…+b_n）；
②S_n≤n（n+2）．
組卷：30引用：1難度：0.5
解析