人教A版必修4高考題單元試卷：第1章 三角函數(shù)（02）

一、選擇題（共18小題）

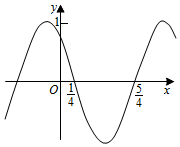• 1．函數(shù)f（x）=cos（ωx+φ）的部分圖象如圖所示，則f（x）的單調(diào)遞減區(qū)間為（　　）

  A．（kπ- 1 4 ，kπ+ 3 4 ），k∈z	B．（2kπ- 1 4 ，2kπ+ 3 4 ），k∈z
  C．（k- 1 4 ，k+ 3 4 ），k∈z	D．（ 2 k - 1 4 ，2k+ 3 4 ），k∈z
  組卷：15243引用：69難度：0.7

  解析

• 2．要得到函數(shù)y=sin（4x-

  π

  3

  ）的圖象，只需要將函數(shù)y=sin4x的圖象（　　）個(gè)單位．

  A．向左平移 π 12	B．向右平移 π 12
  C．向左平移 π 3	D．向右平移 π 3
  組卷：7701引用：99難度：0.9

  解析

• 3．既是偶函數(shù)又在區(qū)間（0，π）上單調(diào)遞減的函數(shù)是（　　）

  A．y=sinx

  B．y=cosx

  C．y=sin2x

  D．y=cos2x
  組卷：2061引用：35難度：0.9

  解析

• 4．為了得到函數(shù)y=sin（2x+1）的圖象，只需把y=sin2x的圖象上所有的點(diǎn)（　　）

  A．向左平行移動(dòng) 1 2 個(gè)單位長(zhǎng)度

  B．向右平行移動(dòng) 1 2 個(gè)單位長(zhǎng)度

  C．向左平行移動(dòng)1個(gè)單位長(zhǎng)度

  D．向右平行移動(dòng)1個(gè)單位長(zhǎng)度
  組卷：2060引用：37難度：0.9

  解析

• 5．將函數(shù)y=sinx的圖象向左平移

  π

  2

  個(gè)單位，得到函數(shù)y=f（x）的函數(shù)圖象，則下列說(shuō)法正確的是（　　）

  A．y=f（x）是奇函數(shù)

  B．y=f（x）的周期為π

  C．y=f（x）的圖象關(guān)于直線x= π 2 對(duì)稱

  D．y=f（x）的圖象關(guān)于點(diǎn)（- π 2 ，0）對(duì)稱
  組卷：2410引用：45難度：0.9

  解析

• 6．為了得到函數(shù)y=sin（x+1）的圖象，只需把函數(shù)y=sinx的圖象上所有的點(diǎn)（　　）

  A．向左平行移動(dòng)1個(gè)單位長(zhǎng)度

  B．向右平行移動(dòng)1個(gè)單位長(zhǎng)度

  C．向左平行移動(dòng)π個(gè)單位長(zhǎng)度

  D．向右平行移動(dòng)π個(gè)單位長(zhǎng)度
  組卷：1235引用：21難度：0.9

  解析

• 7．若點(diǎn)P（sinα-cosα，tanα）在第一象限，則在[0，2π）內(nèi)α的取值范圍是（　　）

  A． （ π 2 ， 3 π 4 ） ∪ （ π ， 5 π 4 ）	B． （ π 4 ， π 2 ） ∪ （ π ， 5 π 4 ）
  C． （ π 2 ， 3 π 4 ） ∪ （ 5 π 4 ， 3 π 2 ）	D． （ π 2 ， 3 π 4 ） ∪ （ 3 π 4 ， π ）
  組卷：984引用：69難度：0.9

  解析

• 8．若0＜a＜1，在[0，2π]上滿足sinx≥a的x的范圍是（　　）

  A．[0，arcsina]	B．[arcsina,π-arcsina]
  C．[π-arcsina,π]	D．[arcsina, π 2 +arcsina]
  組卷：242引用：21難度：0.7

  解析

• 9．為得到函數(shù)

  y

  =

  cos

  （

  2

  x

  +

  π

  3

  ）

  的圖象，只需將函數(shù)y=sin2x的圖象（　　）

  A．向左平移 5 π 12 個(gè)長(zhǎng)度單位

  B．向右平移 5 π 12 個(gè)長(zhǎng)度單位

  C．向左平移 5 π 6 個(gè)長(zhǎng)度單位

  D．向右平移 5 π 6 個(gè)長(zhǎng)度單位
  組卷：9637引用：135難度：0.7

  解析

• 10．在[0，2π]上滿足sinx≥

  1

  2

  的x的取值范圍是（　　）

  A． [ 0 ， π 6 ]

  B． [ π 6 ， 5 π 6 ]

  C． [ π 6 ， 2 π 3 ]

  D． [ 5 π 6 ， π ]
  組卷：2633引用：48難度：0.9

  解析

三、解答題（共4小題）

• 29．已知函數(shù)f（x）=2sin（ωx），其中常數(shù)ω＞0．
  （1）若y=f（x）在

  [

  -

  π

  4

  ，

  2

  π

  3

  ]

  上單調(diào)遞增，求ω的取值范圍；
  （2）令ω=2，將函數(shù)y=f（x）的圖象向左平移

  π

  6

  個(gè)單位，再向上平移1個(gè)單位，得到函數(shù)y=g（x）的圖象，區(qū)間[a,b]（a,b∈R且a＜b）滿足：y=g（x）在[a,b]上至少含有30個(gè)零點(diǎn)，在所有滿足上述條件的[a,b]中，求b-a的最小值．
  組卷：873引用：39難度：0.5

  解析

• 30．設(shè)f（x）=sinxcosx-cos²（x+

  π

  4

  ）．
  （Ⅰ）求f（x）的單調(diào)區(qū)間；
  （Ⅱ）在銳角△ABC中，角A，B，C的對(duì)邊分別為a,b,c,若f（

  A

  2

  ）=0，a=1，求△ABC面積的最大值．
  組卷：10239引用：62難度：0.5

  解析