當前位置：試卷中心 > 試卷詳情

2020-2021學年廣東省汕頭市金平區達濠華僑中學高一（上）期末數學試卷

發布：2024/11/1 23:0:1

1．已知集合A={2，4，6}，B={1，3，4，6}，則A∪B中元素的個數是（　　）
A．2 B．5 C．6 D．7
組卷：61引用：2難度：0.9
解析
2．已知log_a3=m,則a^m的值為（　　）
A．3 B．6 C．9 D．
3
2
組卷：57引用：1難度：0.9
解析
3．“學生甲在云南省”是“學生甲在昆明市”的（　　）
A．充分不必要條件 B．必要不充分條件
C．充要條件 D．既不充分也不必要條件
組卷：114引用：2難度：0.9
解析
4．“?x＜1，x²＜1”的否定是（　　）
A．?x＜1，x²≥1 B．?x≥1，x²≥1 C．?x＜1，x²≥1 D．?x≥1，x²≥1
組卷：68引用：7難度：0.9
解析
5．
sin
5
3
π
的值是（　　）
A．
-
1
2
B．
3
2
C．
1
2
D．
-
3
2
組卷：208引用：2難度：0.8
解析
6．下列函數中，在區間（0，1）上是增函數的是（　　）
A．y=2x B．y=3-x C．
y
=
1
x
D．y=-x²+4
組卷：30引用：3難度：0.8
解析
7．定義運算a⊕b=
a
（
a
≥
b
）
b
（
a
＜
b
）
，則函數f（x）=1⊕2^x的圖象是（　　）
A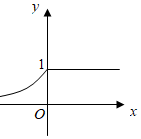． B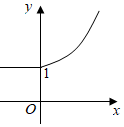． C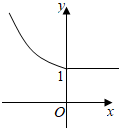． D．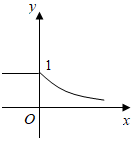
組卷：74引用：9難度：0.9
解析

21．已知函數
f
（
x
）
=
lo
g
2
（
2
2
x
+
1
）
+
ax
．
（1）若f（x）是定義在R上的偶函數，求實數a的值；
（2）在（1）的條件下，若g（x）=f（x）-2，求函數g（x）的零點．
組卷：230引用：3難度：0.3
解析
22．已知函數f（x）為二次函數，不等式f（x）＞0的解集是（1，5），且f（x）在區間[-1，4]上的最小值為-12．
（1）求f（x）的解析式；
（2）設函數f（x）在[t,t+1]上的最小值為g（t），求g（t）的表達式．
組卷：21引用：1難度：0.6
解析

A．充分不必要條件	B．必要不充分條件
C．充要條件	D．既不充分也不必要條件

1．已知集合A={2，4，6}，B={1，3，4，6}，則A∪B中元素的個數是（ ）