2022-2023學年浙江省寧波市北侖中學高一(下)期初數學試卷
發布:2024/6/15 8:0:9
一、單項選擇題:本題共8小題,每小題5分,共40分,在每小題給出的四個選項中,只有一項是符合題目要求的。
-
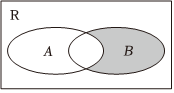 1.已知R是實數集,集合A={x|-3<x+1≤4},B={x|1-x>0},則下圖中陰影部分表示的集合是( )
1.已知R是實數集,集合A={x|-3<x+1≤4},B={x|1-x>0},則下圖中陰影部分表示的集合是( )A.{x|-4<x≤3} B.{x|-4<x<1} C.{x|1<x≤3} D.{x|x≤-4} 組卷:200引用:6難度:0.7 -
2.若對任意1≤x≤2,有x2≤a恒成立,則實數的取值范圍是( )
A.{a|a≤2} B.{a|a≥4} C.{a|a≤5} D.{a|a≥5} 組卷:29引用:4難度:0.8 -
3.已知函數f(x)=sin(ωx+φ)+cos(ωx+φ)(ω>0,φ∈[0,2π)),則“
”是“函數f(x)為奇函數”的( )φ=3π4A.充分不必要條件 B.必要不充分條件 C.充分必要條件 D.既不充分也不必要條件 組卷:123引用:2難度:0.7 -
4.已知函數f(x)=log3x+3x,g(x)=3x+3x,h(x)=x3+3x的零點分別x1,x2,x3,則x1,x2,x3的大小關系為( )
A.x2<x3<x1 B.x1<x2<x3 C.x2<x1<x3 D.x3<x2<x1 組卷:700引用:3難度:0.6 -
5.設函數
,已知f(x)在[0,2π]上有且僅有4個零點,且f(x)圖象的對稱中心為f(x)=sin(ωx+π3)(ω>0),則(π3,0)=( )f(π6)A. 12B. 32C. -12D. -32組卷:109引用:2難度:0.7 -
6.函數f(x)=2|x|sin2x的圖像最有可能的是( )
A. 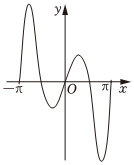
B. 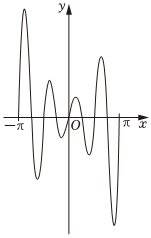
C. 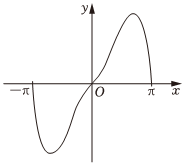
D. 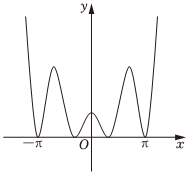 組卷:30引用:3難度:0.7
組卷:30引用:3難度:0.7 -
7.已知關于x的不等式ax2+bx+4>0的解集為
,其中m<0,則(-∞,m)∪(4m,+∞)的最小值為( )ba+4bA.-4 B.4 C.5 D.8 組卷:978引用:22難度:0.6
四、解答題:本題共6個小題,共70分,解答應寫出文字說明,證明過程或演算步驟。
-
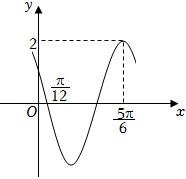 21.已知函數f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的部分圖象如圖所示.
21.已知函數f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的部分圖象如圖所示.
(1)求f(x)的解析式;
(2)設.若關于x的不等式g2(x)-(3m+2)g(x)-m-23≤0恒成立,求m的取值范圍.g(x)=f(x)+23cos(π6-2x)+1組卷:303引用:4難度:0.6 -
22.已知函數g(x)=ax2-2ax+1+b(a,b≥0)在x∈[1,2]時有最大值1和最小值0,設
.f(x)=g(x)x
(1)求實數a,b的值;
(2)若不等式f(log2x)-2klog2x≤0在上恒成立,求實數k的取值范圍;x∈[18,14]
(3)若關于x的方程有三個不同的實數解,求實數m的取值范圍.f(|2x-1|)+2m|2x-1|-3m-1=0組卷:663引用:12難度:0.4


