2021-2022學年廣東省深圳市龍城高級中學高二（下）期中數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．

  A

  2

  4

  +

  C

  2

  10

  =（　　）

  A．55

  B．57

  C．100

  D．110
  組卷：146引用：3難度：0.9

  解析

• 2．雙曲線

  y

  2

  3

  -

  x

  2

  =

  1

  的漸近線方程是（　　）

  A． 3 x ± y = 0

  B． 3 x ± 3 y = 0

  C．x±y=0

  D． x ± 2 y = 0
  組卷：127引用：3難度：0.7

  解析

• 3．有一個人在打靶中，連續射擊2次，事件“至少有1次中靶”的對立事件是（　　）

  A．至多有1次中靶	B．2次都中靶
  C．2次都不中靶	D．只有1次中靶
  組卷：935引用：32難度：0.9

  解析

• 4．已知隨機變量X，Y滿足X+Y=8，且X～B（10，0.6），則D（X）+E（Y）=（　　）

  A．2.4

  B．3.4

  C．4.2

  D．4.4
  組卷：119引用：2難度：0.7

  解析

• 5．良好的睡眠是保證高中學生良好學習狀態的基礎，為了解某校高三學生的睡眠狀況，該校調查了高三年級1200名學生的睡眠時間（單位：小時），經調查發現，這1200名學生每天的睡眠時間X～N（8，1），則每天的睡眠時間為5～6小時的學生人數約為（　　）（結果四舍五入保留整數）
  （附：若X～N（μ，σ²），則P（μ-σ≤X≤μ+σ）≈0.6827，P（μ-2σ≤X≤μ+2σ）≈0.9545，P（μ-3σ≤X≤+3σ）≈0.9973．）

  A．163

  B．51

  C．26

  D．20
  組卷：303引用：6難度：0.8

  解析

• 6．第24屆冬奧會奧運村有智能餐廳A、人工餐廳B，運動員甲第一天隨機地選擇一餐廳用餐，如果第一天去A餐廳，那么第二天去A餐廳的概率為0.7；如果第一天去B餐廳，那么第二天去A餐廳的概率為0.8．運動員甲第二天去A餐廳用餐的概率為（　　）

  A．0.75

  B．0.7

  C．0.56

  D．0.38
  組卷：1882引用：21難度：0.8

  解析

• 7．

  （

  x

  3

  +

  1

  x

  -

  1

  ）

  4

  的展開式中x⁵的系數為（　　）

  A．12

  B．-12

  C．6

  D．-6
  組卷：558引用：2難度：0.7

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

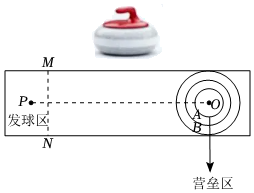• 21．冰壺是2022年2月4日至2月20日在中國舉行的第24屆冬季奧運會的比賽項目之一．冰壺比賽的場地如圖所示，其中左端（投擲線MN的左側）有一個發球區，運動員在發球區邊沿的投擲線MN將冰壺擲出，使冰壺沿冰道滑行，冰道的右端有一圓形的營壘，以場上冰壺最終靜止時距離營壘區圓心O的遠近決定勝負．甲、乙兩人進行投擲冰壺比賽，規定冰壺的重心落在圓O中，得3分，冰壺的重心落在圓環A中，得2分．冰壺的重心落在圓環B中，得1分，其余情況均得0分．已知甲、乙投擲冰壺的結果互不影響．甲、乙得3分的概率分別為

  1

  3

  ，

  1

  4

  ；甲、乙得2分的概率分別為

  2

  5

  ，

  1

  2

  ；甲、乙得1分的概率分別為

  1

  5

  ，

  1

  6

  ．
  （1）求甲、乙兩人所得分數相同的概率；
  （2）設甲、乙兩人所得的分數之和為X，求X的分布列和期望．
  組卷：662引用：15難度：0.6

  解析

• 22．設函數

  f

  （

  x

  ）

  =

  （

  x

  +

  a

  ）

  lnx

  -

  a

  2

  （

  x

  +

  1

  ）

  ．
  （1）若a=0，求f（x）的單調區間；
  （2）若f（x）在區間（2，+∞）單調遞增，求整數a的最大值．
  組卷：128引用：2難度：0.3

  解析