2021-2022學年山東省淄博十一中高一（上）期中數學試卷

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．已知集合U={1，2，3，4，5，6}，A={2，4}，B={1，3，4}，則（?_UB）∩A=（　　）

  A．{2）

  B．{4}

  C．{1，3}

  D．{5，6}
  組卷：16引用：2難度：0.8

  解析

• 2．已知a＞b,則（　　）

  A．a2＞b2

  B．a3＞b3

  C．|a|＞|b|

  D．ac2＞bc2
  組卷：45引用：5難度：0.8

  解析

• 3．已知函數f（x）的定義域為（0，2），則函數

  g

  （

  x

  ）

  =

  f

  （

  x

  -

  2

  ）

  x

  -

  3

  的定義域為（　　）

  A．（3，+∞）

  B．（2，4）

  C．（3，4）

  D．（-2，3）
  組卷：102引用：5難度：0.7

  解析

• 4．在△ABC中，“AB=AC”是“△ABC為等腰三角形”的（　　）

  A．充要條件	B．必要不充分條件
  C．充分不必要條件	D．既不充分也不必要條件
  組卷：97引用：3難度：0.8

  解析

• 5．國慶期間，高一某班35名學生去電影院觀看了《長津湖》《我和我的父輩》這兩部電影中的一部或兩部．其中有23人觀看了《長津湖》，有20人觀看了《我和我的父輩》，則同時觀看了這兩部電影的人數為（　　）

  A．8

  B．10

  C．12

  D．15
  組卷：18引用：1難度：0.8

  解析

• 6．已知函數

  f

  （

  x

  ）

  =

  （ 2 - a ） x , x ＜ 1

  x a ， x ≥ 1

  是定義在R上的增函數，則a的取值范圍是（　　）

  A．（0，1]

  B．[1，2）

  C．（-∞，2）

  D．（0，+∞）
  組卷：607引用：6難度：0.6

  解析

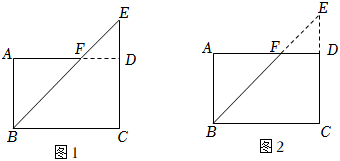• 7．數學里有一種證明方法叫做Proof without words,也被稱為無字證明，是指僅用圖象而無需文字解釋就能不證自明的數學命題．由于這種證明方法的特殊性，無字證明被認為比嚴格的數學證明更為優雅與有條理．在同一平面內有形狀、大小相同的圖1和圖2，其中四邊形ABCD為矩形，三角形BCE為等腰直角三角形，設AB=

  a

  ，BC=

  b

  （a＞0，b＞0），則借助這兩個圖形可以直接無字證明的不等式是（　　）

  A． a + b 2 ≥ ab （ a ＞ 0 ， b ＞ 0 ）	B． a + b 2 ≤ a 2 + b 2 2 （ a ＞ 0 ， b ＞ 0 ）
  C． 2 ab a + b ≤ ab （ a ＞ 0 ， b ＞ 0 ）	D． a 2 + b 2 ≥ 2 ab （ a ＞ 0 ， b ＞ 0 ）
  組卷：58引用：1難度：0.8

  解析

四、解答題：本題共6小題，共70分.解答應寫出必要的文字說明、證明過程或演算步驟.

• 21．某科研機構為了研究某種藥物對某種疾病的治療效果，準備利用小白鼠進行科學試驗．研究發現，藥物在血液內的濃度與時間的關系因使用方式的不同而不同．若使用注射方式給藥，則在注射后的4小時內，藥物在白鼠血液內的濃度y₁（單位：毫克/升）與時間t（單位：小時）滿足關系式y₁=5-at（a＞0，a為常數）；若使用口服方式給藥，則藥物在白鼠血液內的濃度y₂（單位：毫克/升）與時間t（單位：小時）滿足關系式y₂=

  2 t ， 0 ＜ t ＜ 1 ，

  5 - 4 t ， 1 ≤ t ≤ 4 ．

  現對小白鼠同時進行注射和口服該種藥物，且注射藥物和口服藥物的吸收與代謝互不干擾．假設同時使用兩種方式給藥后，小白鼠血液中藥物的濃度等于單獨使用每種方式給藥的濃度之和．
  （1）若a=1，求4小時內，該小白鼠何時血液中藥物的濃度最高，并求出最大值；
  （2）若要使小白鼠在用藥后4小時內血液中的藥物濃度都不低于4毫克/升，求正數a的取值范圍．
  組卷：209引用：9難度：0.5

  解析

• 22．設函數f（x）的定義域為D，若存在正實數a,使得對于任意x∈D，總有x+a∈D，且f（x+a）＞f（x），則稱f（x）是D上的“a距增函數”．
  （1）判斷函數f（x）=x²+x是否為（0，+∞）上的“1距增函數”，并說明理由；
  （2）已知f（x）是定義在R上的奇函數，且當x＞0時，f（x）=x+b.若f（x）為R上的“2021距增函數”，求b的取值范圍．
  組卷：17引用：1難度：0.4

  解析