2022-2023學(xué)年江西省景德鎮(zhèn)一中高二(下)期中數(shù)學(xué)試卷
發(fā)布:2024/5/29 8:0:9
一、單選題:本題共8小題,共40分.在每小題給出的四個選項中,只有一項符合題目要求.
-
1.對四組數(shù)據(jù)進(jìn)行統(tǒng)計,獲得以下散點圖,關(guān)于其相關(guān)系數(shù)的比較,正確的是( )
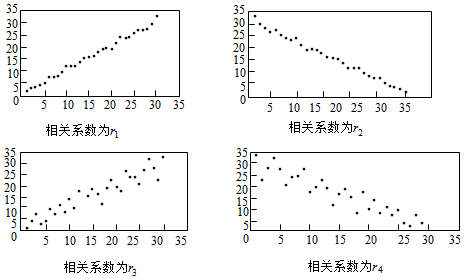
A.r2<r4<0<r3<r1 B.r4<r2<0<r1<r3 C.r4<r2<0<r3<r1 D.r2<r4<0<r1<r3 組卷:1799引用:51難度:0.9 -
2.設(shè)隨機(jī)變量X~N(μ,7),若P(X<2)=P(X>6),則( )
A.μ=4,D(X)=7 B.μ=8,D(X)=7 C.μ=4, D(X)=7D.μ=8, D(X)=7組卷:65引用:2難度:0.8 -
3.(2+
)(1-x)10展開式中的常數(shù)項為( )1xA.12 B.8 C.-8 D.-12 組卷:90引用:4難度:0.7 -
4.南宋數(shù)學(xué)家楊輝為我國古代數(shù)學(xué)研究作出了杰出貢獻(xiàn),他的著名研究成果“楊輝三角”記錄于其重要著作《詳解九章算法》,該著作中的“垛積術(shù)”問題介紹了高階等差數(shù)列.以高階等差數(shù)列中的二階等差數(shù)列為例,其特點是從數(shù)列中的第二項開始,每一項與前一項的差構(gòu)成等差數(shù)列.若某個二階等差數(shù)列的前4項為:2,3,6,11,則該數(shù)列的第10項為( )
A.84 B.83 C.82 D.81 組卷:34引用:2難度:0.7 -
5.已知數(shù)列{an}中,a1=1,an+1=4an-6,則a2023=( )
A.-42023+2 B.-42023-2 C.-42022+2 D.-42022-2 組卷:157引用:2難度:0.7 -
6.現(xiàn)有6名同學(xué),其中有甲、乙、丙、丁四人,要求甲、乙兩人相鄰,且丙和甲不相鄰,同時丁需排在甲前面(兩人不一定相鄰),則總共的排列種數(shù)為( )
A.96 B.98 C.192 D.196 組卷:70引用:2難度:0.5 -
7.現(xiàn)做如下定義:對一個三位數(shù)來說,如果其中間一位數(shù)比首尾的數(shù)字小,則稱它為“凹數(shù)”,如果其中間一位數(shù)比首尾的數(shù)字大,則稱其為“凸數(shù)”.現(xiàn)從1至7共7個數(shù)中,選取3個不同的數(shù)排成三位數(shù),記其中“凹數(shù)”有m個,“凸數(shù)”有n個,則m+n=( )
A.135 B.140 C.150 D.160 組卷:60引用:2難度:0.5
四、解答題:本大題共6小題,共70分.
-
21.某工廠生產(chǎn)的10件產(chǎn)品中含有n(2≤n≤7)件次品,從中一次任取5件,其中次品恰有X件.
(1)若n=5,求取出的產(chǎn)品中次品數(shù)量不超過1件的概率.
(2)記f(n)=P(X=2),求當(dāng)n為何值時,f(n)取得最大值.組卷:38引用:2難度:0.5 -
22.已知數(shù)列{an}滿足
,an+1=a2n2021+an.a1=12
(1)證明:數(shù)列{an}為遞增數(shù)列.
(2)證明:a2022<1
(3)證明:a2023>1組卷:22引用:2難度:0.5


