2022年黑龍江省哈爾濱九中高考數學四模試卷（理科）

一、選擇題（本題共12小題，每小題5分，在下列各題的四個選項中，只有一項是最符合題意的）

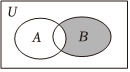• 1．已知全集U=R，集合A={0，3，4}，集合B={0，2，4，5}，則圖中的陰影部分表示的集合為（　　）

  A．{2，5}

  B．{3}

  C．{0，4}

  D．{0，5}
  組卷：77引用：2難度：0.8

  解析

• 2．某種包裝的大米質量ξ（單位：kg）服從正態分布ξ～N（10，σ²），根據檢測結果可知P（9.98≤ξ≤10.02）=0.98，某公司購買該種包裝的大米3000袋．大米質量在10.02kg以上的袋數大約為（　　）

  A．10

  B．20

  C．30

  D．40
  組卷：56引用：1難度：0.8

  解析

• 3．歐拉是18世紀最偉大的數學家之一，在很多領域都有杰出的貢獻．由《物理世界》發起的一項調查表明，人們把歐拉恒等式“e^iπ+1=0”與麥克斯韋方程組并稱為“史上最偉大的公式”．其中，歐拉恒等式是歐拉公式：e^iθ=cosθ+isinθ的一種特殊情況．由歐拉公式，復數z滿足（e^2022πi+i）?z=-2i,則z的虛部是（　　）

  A．i

  B．1

  C．-i

  D．-1
  組卷：16引用：2難度：0.7

  解析

• 4．記△ABC的內角A，B，C的對邊分別為a,b,c,

  sin

  C

  =

  21

  7

  ，b=3，c=2，則cosB的值為（　　）

  A． - 7 14

  B． 7 14

  C． ± 7 14

  D． ± 7 7
  組卷：114引用：2難度：0.8

  解析

• 5．觀察下列等式，1³=1²，1³+2³=3²，1³+2³+3³=6²，1³+2³+3³+4³=10²，根據上述規律，1³+2³+3³+4³+5³+6³+…+n³=（　　）

  A． n 4 + n 3 + 2 n 2 4

  B． n 4 + 2 n 3 + n 2 4

  C． n 4 - n 3 + n 2 4

  D． n 4 - 2 n 3 + n 2 4
  組卷：44引用：6難度：0.6

  解析

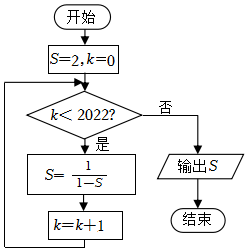• 6．執行如圖所示的程序框圖，則輸出的S=（　　）

  A．2

  B．1

  C． 1 2

  D．-1
  組卷：140引用：7難度：0.7

  解析

• 7．設m,n是空間兩條不同直線，α，β是空間兩個不同平面，則下列選項中正確的是（　　）

  A．當α∥β時，“n⊥α”是“n⊥β”的充分不必要條件

  B．當m?α時，“m⊥β”是“α⊥β”的充分不必要條件

  C．當m?α時，“n∥α”是“m∥n”的必要不充分條件

  D．當α⊥β時，“m∥α”是“m∥β”的必要不充分條件
  組卷：19引用：1難度：0.6

  解析

三、解答題：（共70分．解答寫出文字說明，證明過程或演算步驟，第17—21題為必考題，每個試題考生都必須作答，第22，23為選考題，考生根據要求作答．）

• 22．以直角坐標系的原點O為極點，x軸的非負半軸為極軸由建立極坐標系，曲線C的參數方程為

  x = 3 t

  y = 2 t 2 + 1

  （t為參數），直線l的極坐標方程為

  ρcos

  （

  π

  3

  +

  θ

  ）

  =

  3

  3

  2

  ．
  （1）已知點M（a,9）在曲線C上，求a的值；
  （2）設點P為曲線C上一點，求點P到直線l距離的最小值．
  組卷：77引用：3難度：0.7

  解析

• 23．已知函數f（x）=|x+1|-|2x-3|．
  （1）求不等式f（x）≥1的解集；
  （2）若f（x）的最大值為m,且

  lo

  g

  a

  b

  =

  -

  4

  5

  m

  ，求a+4b最小值．
  組卷：46引用：2難度：0.6

  解析